A logarithm is an exponent.
In the example shown at the right, 3 is the exponent to which the
base 2 must be raised to create the answer of 8, or 23 = 8.
In this example, 8 is called the antilogarithm base 2 of 3.
logpic
Try to remember the "spiral" relationship between the values as shown at the right. Follow the arrows starting with base 2 to get the equivalent exponential form, 23 = 8.
logrule

bullet A logarithm base b of a positive number x is such that:
for b > 0, b≠ 1, logb x = y if and only if by = x.
The log bx is read "log base b of x".
The logarithm y is the exponent to which b must be raised to get x.

Logarithms with base 10 are called common logarithms. When the base is not indicated, base 10 is implied.
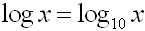log27
Logarithms with base e are called
natural logarithms. Natural logarithms
are denoted by ln.
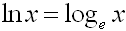log28

dividerdash

green
hintgal
Logarithms with base 10 are called common logarithms and are written without the 10 showing.
The log key will calculate common
(base 10) logarithms. 		logkey
Logarithms with the base e are called natural logarithms and are written using the notation ln(x).
The ln key will calculate natural
(base e) logarithms.		 lnkey
For "other bases" use the change of base formula:
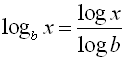
logcalcformula
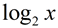
log2f
is entered as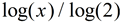log22g

Origins of Change of Base Formula:
log21
Set = x.
l0g21
Convert to exponential form.
log22
Take common log of both sides.
log23
User power rule.
log24
Divide by log b.
Change of Base Formula: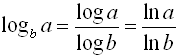log97
Calculator Entry:

log17    arrowred   logpic


The logBASE( operation template can also be used.
To load the template go to
MATH → arrow down to A: logBASE(.
For more options, see link below:
ti84c

For more help with logarithms on your calculator, click here.


dividerdash

Properties of Logarithms
Using the properties of exponents, we can arrive at the properties of logarithms.
Properties of
Exponents:
log30
Let's find the connection!
log31
Similar investigations lead to the other logarithm properties.
Properties of
Logarithms:
log125
log126
logr
Also, log44

These log properties remain the same when
working with the natural log.
orangearrow
Remember:    ln 1 = 0    and    ln e = 1
log127

dividerdash

Examples:

1.
 Write le1 in exponential form. Solution: le1a
2.
 Write le2in logarithmic form. Solution: le2a
3.
 Evaluate: le3 Solution: le3a
If using your calculator, remember to use the change of base formula and enter log 1 / log 3.
4.
 What is the value of x? le4 Solution: le4a
5.
 Write in expanded form: le5
(Apply the "properties of logs" rules.)		 Solution: le5a
6.
 Write in expanded form: le6 Solution:le6a
7.

Express as a single logarithm:le7

(Apply the properties of logs rules in reverse)

 Solution: le7a
8.
 Express as a single logarithm:le8
 Solution: le8a
9.
 Using properties of logarithms, show thatle9 Solution:
le9a
10.
 Using properties of logs, solve for x.le10
 Solution:
le10a


divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".