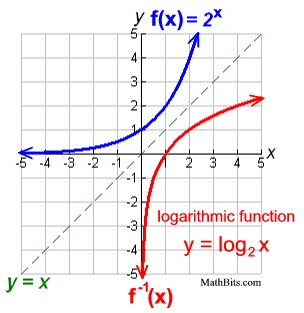
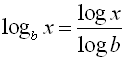Let's start by taking a look at the inverse of the exponential function, f (x) = 2x .
In Algebra 1, you saw that when working with the inverse of a function, the inputs (x) and outputs (y) exchange places, and that the inverse will be a reflection over the identity line y = x.
f (x) = 2x
x |
-2 |
-1 |
0 |
1 |
2 |
3 |
f(x) |
¼ |
½ |
1 |
2 |
4 |
8 |
The inverse: f -1 (x)
x |
¼ |
½ |
1 |
2 |
4 |
8 |
f-1(x) |
-2 |
-1 |
0 |
1 |
2 |
3 |
This new inverse function is called a logarithmic function and is expressed by the equation:
y = log2 (x) |
|
The composition of a function with its inverse returns the starting value,
x.
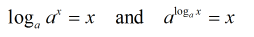
This concept will be used to solve equations involving exponentials and logarithms.

Now that we have a basic idea of a logarithmic function, let's take a closer look at its graph.
|
The logarithmic function is the function
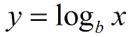 where b is any number such that b > 0, b≠ 1, and x > 0.
where b is any number such that b > 0, b≠ 1, and x > 0.
The function is read "log base b of x".
The logarithm y is the exponent to which b must be raised to get x.
|
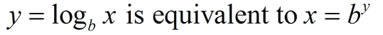 The inverse of y = bx, will be x = by (where the x and y change places).
The inverse of y = bx, will be x = by (where the x and y change places).
Note that y (the logarithm) is actually an exponent. |
|
Let's examine the function: 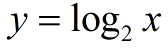
The value of b (the 2) is referred to as the base of the logarithm.
Notice that x must be positive.
|
|
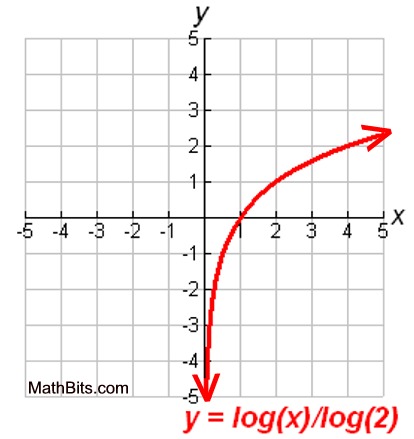 |
Most logarithmic graphs resemble this same basic shape. Notice that this graph is very, very close to the y-axis but does not cross it. The x-values of this graph are always positive, and the y-values increase as the graph progresses to the right (as seen in the above graph).
Note: In a linear graph, the "rate of change" remains the same across the entire graph.
In a logarithmic graph, the "rate of change" increases (or decreases) across the graph.
Entering logarithms on the graphing calculator |
|
|
For help with logarithms on
your calculator,
click here.
|
|
|
The log key will calculate common
(base 10) logarithms. |
 |
The ln key will calculate natural
(base e) logarithms. |
 |
|
For " other bases" use the following "change of base" conversion:
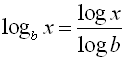
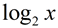
is entered as
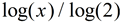
Or use logBASE( template at MATH → arrow down to A:logBASE(.
|
|
Common Logarithm
Base 10 logarithm
log10(x) abbreviated log(x) |
|
Natural Logarithm
Base e logarithm
loge(x) abbreviated ln(x) |
|

Characteristics of Logarithmic Functions |
|
|
The graphs of functions of the form 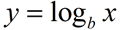 have certain characteristics in common.
have certain characteristics in common.
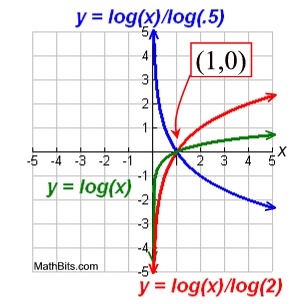 Logarithmic functions are one-to-one functions.
Logarithmic functions are one-to-one functions.
|
• graph crosses the x-axis at (1,0)
• when b > 1, the graph increases
• when 0 < b < 1, the graph decreases
• the domain is all positive real numbers (never zero)
• the range is all real numbers
• graph passes the vertical line test for functions
• graph passes the horizontal line test for functional inverse.
• graph is asymptotic to the y-axis - gets very, very close to the y-axis but, in this case, does not touch it or cross it. |

Transformations on Logarithmic Functions |
|
|
We know that transformations have the ability to move functions by sliding them, reflecting them, stretching them, and shrinking them. Let's see how these changes will affect the logarithmic function:
Parent function: 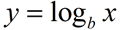
y = a logbx
Stretch (|a| > 1):
Compress or Shrink
(0 < |a| < 1):
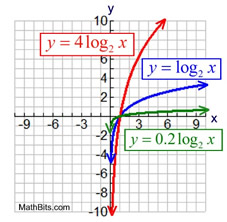
Domain: x > 0
Range: x ∈ Real numbers
|
y = a logbx
Reflection (a < 0) in x-axis:
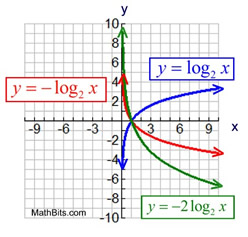
Domain: x > 0
Range: x ∈ Real numbers
|
Translation y = logb(x - h) + k
horizontal by h: vertical by k:
Domain: x > h
Range: x ∈ Real numbers
|
All 3 transformations combined: y = a logb(x - h) + k

Intercepts of Logarithmic Functions |
|
|
By examining the nature of the logarithmic graph, we have seen that the parent function will stay to the right of the x-axis, unless acted upon by a transformation.
• The parent function, y = logb x, will always have an x-intercept of one, occurring at the ordered pair of (1,0).
There is no y-intercept with the parent function since it is asymptotic to the y-axis (approaches the y-axis but does not touch or cross it).
• The transformed parent function of the form y = a logb x, will also always have a x-intercept of 1, occurring at the ordered pair of (1, 0). Note that the value of a may be positive or negative.
Like the parent function, this transformation will be asymptotic to the y-axis, and will have no y-intercept.
•
If the transformed parent function includes a vertical or horizontal shift, all bets are off. The horizontal shift will affect the possibility of a y-intercept and the vertical shift will affect the x-intercept. In this situation, you will need to examine the graph carefully to determine what is happening. |
 |
End Behavior of Logarithmic Functions |
|
|
The end behavior of a logarithmic graph also depends upon whether you are dealing with the parent function or with one of its transformations.
• The end behavior of the parent function is consistent.
As x approaches infinity, the y-values slowly get larger, approaching infinity. As x approaches 0 from the right (denoted as x → 0+), the y-values approach negative infinity. |
|
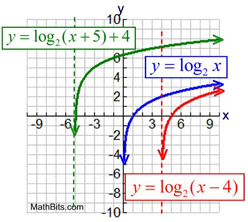
• The end behavior of a transformed parent function is not always consistent, but is dependent upon the nature of the transformation. Consider this example:
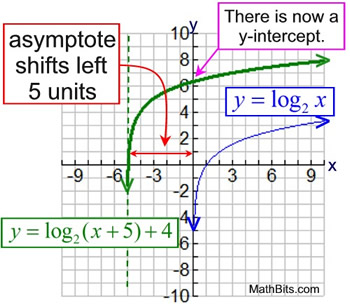 |
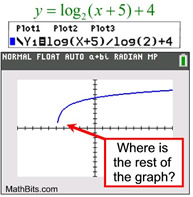
For the transformed equation
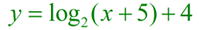
the horizontal shift of +5 will push the
asymptote line to the left five units.
Thus the end behavior will be:

The y-intercept, where x = 0, is
y = log 2 (0 + 5) + 4 ≈ 6.321928095.
The x-intercept, where y = 0, is
approximately -4.94 (from the graph's table).
|
|
|
|

Don't confuse log graphs
with square root graphs.
At fist glance, these two graphs appear to be similar. But the square root graph is actually ending, while the log graph is not.
|
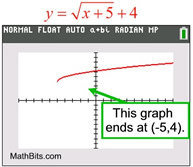 |
| On the logarithmic graph, the calculator is "trying" to plot points on the graph to the left. But the graph is SO CLOSE to the asymptote of x = -5, there is no room to put additional pixels before it crosses over the asymptote. Plotting points "straight" down would violate the graph being a function, and the TI-84+ plots functions. |