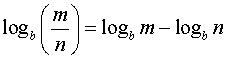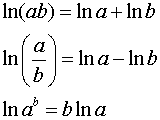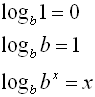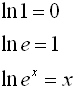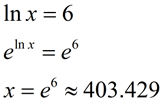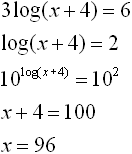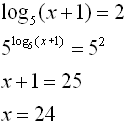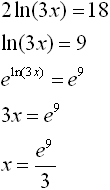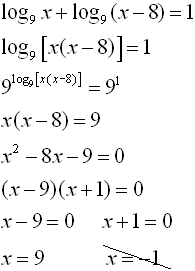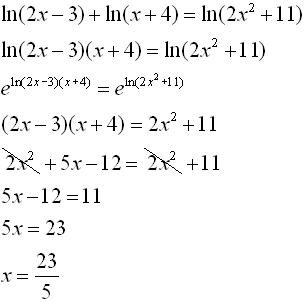A logarithmic equation can be solved using the properties of logarithms along with its inverse relationship with exponentials.
leanguy
Properties of Logarithms:
log125
log126
logr
log127

bullet To solve most logarithmic equations:
1. Isolate the logarithmic expression
     (you may need to use the properties of logarithms to create one
     logarithmic term).
2. Rewrite in exponential form (with a common base)
3. Use the inverse relationship with exponentials:
 logNg(where a > 0, a ≠1, and logax is defined).
4. Solve for the variable.
5. Check for possible extraneous solutions.
      Remember the domain of logarithmic functions is x > 0.
Things to remember
about logs:
log1
log2

Remember that y = ex and
y = ln x are inverse functions.

examples
 
Solve for x:
Answer
1.
ll1
ll1as
 • Take e of both sides to eliminate the ln
• Remember that ex and ln x are inverse function (one undoes the other).
2.
ll2
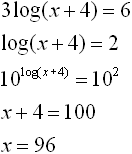logseq
• Isolate the log expression

• Choose base 10 to correspond with log (base 10)

• Apply composition of inverses and solve.
3.
ll3
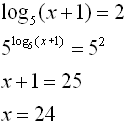logs71 • Choose base 5 to correspond with the log base of 5.
4.
ll4
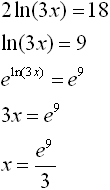logs73 • Isolate the ln expression first.
5.
 ll5
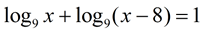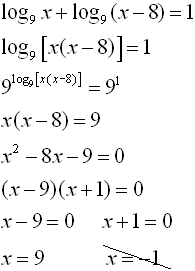logs75 beware
• You will need to use the log properties to express the two terms on the left as a single term.

• Remember that log of a negative value is not a real number and is not considered a solution.
6.
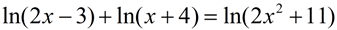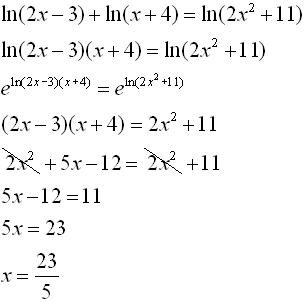 ll6 logs77
7.
 Using your graphing calculator, solve for x to the nearest hundredth.
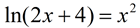
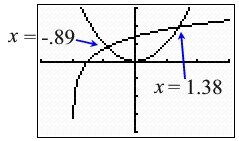
ll7 Method 2: Place the left side of the equation into Y1 and the right side into Y2. Under the CALC menu, use #5 Intersect to find where the two graphs intersect.
loggraph2 		Method 1: Rewrite so the equation equals 0.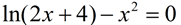ll7b
Find the zeros of the function.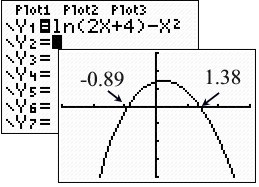loggraph
Both values are solutions, since both values allow for the ln of a positive value.



ti84c

For help with logarithms on
your calculator,
click here.

 

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".