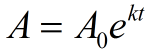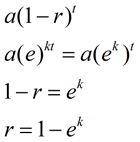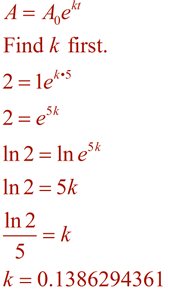|
The following two function formulas can be easily used to illustrate the concepts of growth and decay in applied situations. If a quantity grows by a fixed percent at regular intervals, the pattern can be depicted by these functions.
Exponential Growth:
y = a(1 + r)x |
|
Exponential Decay:
y = a(1 - r)x |
|
Remember that the original exponential formula was y = abx.
You will notice that in these new growth and decay functions,
the b value (growth factor) has been replaced either by (1 + r) or by (1 - r).
The growth "rate" (r) is determined as b = 1 + r.
The decay "rate" (r) is determined as b = 1 - r
a = initial value (the amount before measuring growth or decay)
r = growth or decay rate (most often represented as a percentage and expressed as a decimal)
x = number of time intervals that have passed
|
Example 1: The population of HomeTown is 2016 was estimated to be 35,000 people with an annual rate of increase of 2.4%.
a) What is the growth factor for HomeTown?
After one year the population would be 35,000 + 0.024(35000).
By factoring, we have 35000(1 + 0.024) or 35000(1.024).
The growth factor is 1.024. (Remember that growth factor is greater than 1.)
b) Write an equation to model future growth.
y = abx = a(1.024)x = 35000(1.024)x
c) Use the equation to estimate the population in 2020 to the nearest hundred people.
y = 35000(1.024)4 ≈ 38,482.91 ≈ 38,500 |
|

Most naturally occurring phenomena grow continuously. For example, bacteria will continue to grow over a 24 hours period, producing new bacteria which will also grow. The bacteria do not wait until the end of the 24 hours, and then all reproduce at once.
The exponential e is used when modeling continuous growth that occurs naturally such as populations, bacteria, radioactive decay, etc.
You can think of e like a universal constant representing how fast you could possibly grow using a continuous process. And, the beauty of e is that not only is it used to represent continuous growth, but it can also represent growth measured periodically across time (such as the growth in Example 1).
In Algebra 2, the exponential e will be used in situations of continuous growth or decay. The following formula is used to illustrate continuous growth and decay. If a quantity grows continuously by a fixed percent, the pattern can be depicted by this function.
Continuous Exponential Growth or Decay
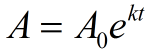
A = ending value (amount after growth or decay)
A0 = initial value (amount before measuring growth or decay)
e = exponential e = 2.71828183...
k = continuous growth rate (also called constant of proportionality)
(k > 0, the amount is increasing (growing); k < 0, the amount is decreasing (decaying))
t = time that has passed |
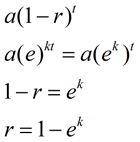 |
If we compare this new formula to our previous exponential decay formula (or growth formula), we can see how ek is related to the rate of decay, r, (or growth). |
Example: A strain of bacteria growing on your desktop doubles every 5 minutes. Assuming that you start with only one bacterium, how many bacteria could be present at the end of 96 minutes?
(bacteria continuously grow)
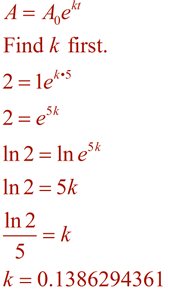 |
Now, form the equation using this k value, and solve the problem using the time of 96 minutes.
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|