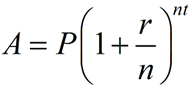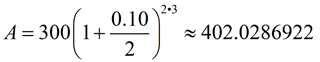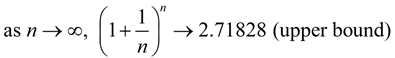You were finding simple interest when you used the formula I = P x R x T.
(Interest = Principal x Rate x Time) When working with simple interest, your total accrued amount (A), or principal + interest, will be: A = P + I = P + Prt = P(1 + rt). Example: Karla invests $300 at a simple annual interest rate of 10% for 3 years. At the end of three years, Karla will have earned $90 in interest. I = P x R x T = 300 x 0.10 x 3 = $90.
Example: Karla invests $300 compounded annually at a rate of 10% for 3 years. At the end of three years, Karla will have earned $99.30 in interest and have $399.30 in her account.
We just saw that compound interest will get us more money. But won't we get even MORE money if we compound it more often - say every 6 months, instead of once a year?
Yes, compounding more often will increase the interest earned. So, this new formula will allow for multiple time periods, n, per year, t, for the compounding to occur.
Example: Karla invests $300 compounded every 6 months at a rate of 10% for 3 years. At the end of three years, Karla will have $402.03 in her account.
If decreasing the time periods between the compounding will increase the interest earned, then the best option is to have the interest compounded continuously (every second, every nanosecond, instantaneously). We want n (n = number of times per year compounded) to approach infinity. Then every instant, the interest is hypothetically computed and added to the balance. While this is not actually possible, continuous compounding is defined as "the upper bound of compound interest". As you compound more often, the effective annual rate increases. But it will not increase indefinitely. It will tend to a finite value which is an upper bound that is approached as the frequency of compounding increases. When the effective annual rate is at this upper bound, it is said that the interest is being compounded continuously. When the interest of an annual rate of 1 is compounded n time a year, we have Example: Karla invests $300 continuously compounded at a rate of 10% for 3 years. At the end of three years, Karla will have $404.96 in her account.
When the upper bound is being used, we achieve the maximum amount of money possible under the given conditions.
It has been reported that Albert Einstein once said that
Topical Outline | Algebra 2 Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|