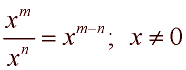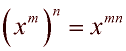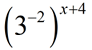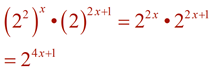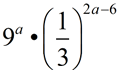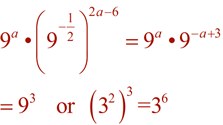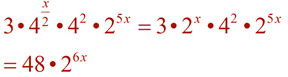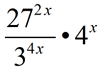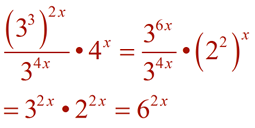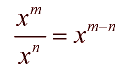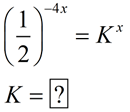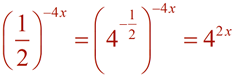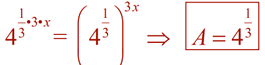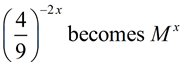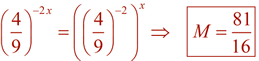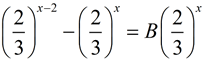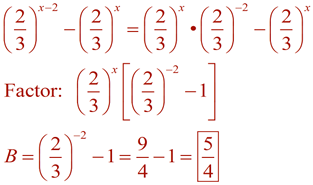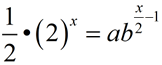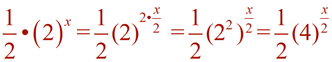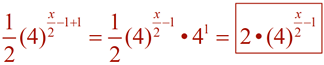bullet An exponential expression is one which contains an exponent.

When working with exponential expressions, you will need to remember the rules that pertain to dealing with exponents. Algebra 2 will expect you to use these rules (forward and backward) in a variety of situations. Primarily, you will need to remember the following rules:

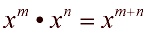Product Rule: prodrule
Quotient Rule:
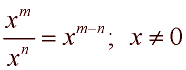quotrule
Power to Power Rule:
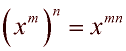powerrulw
Product to Power Rule:
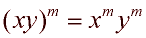pprule


Simplifying Exponential Expressions:
 
Simplify the following expressions into the form a•bx.
1.
 ee1 Solution:    ee1a Rule: prodrule
2.
 dd2 Solution:     ee2a Rule: powerrulw
3.
 ee31 Solution:  Get a common base.  ee3a Rule: powerrulw
Rule: prodrule
4.
 ee41 Solution: Get a common base.
  ee4a		 Rule: powerrulw
Rule: prodrule
5.
 ee5 Solution: Simplify 2nd term.   
ee5a		 Rule: powerrulw
Rule: prodrule
6.
 ee6 Solution:   Simplify quotient.  ee6a

Rule: powerrulw
Rule: shrule
Rule: pprule



Re-writing Exponential Expressions:
 
You may be asked to re-write an exponential expression in a simpler form, as seen above, to make it more easily readable. Or you may be asked to re-write the expression into a more obscure form to reveal pertinent information about a concept or about the expression itself.
1.
 Find K.
rw1
 Solution:   Let's see if we can re-write the left-hand side to contain an exponent of simply x.
rw1a
Better, but not good enough. If we cannot simplify the left-side further, how can we manipulate what we have into becoming K x ? rw1aa
2.
 To rewrite
rw2a,
A will be _____.
 Solution:    We need the exponent on 4 to contain a 3. We can introduce 3•1/3 (which equals 1) without changing the expression.
rw2aa1
3.
 Find M, such that
rwaa		 Solution:   Separate the exponent to produce the x alone.
 rw3a
4.
 Find B.rw4 Solution:  Re-write the first term and then factor. 
rw4a  
5.
 Find a and b:
rw55		 Solution: Yikes! Let's work on that exponent first. rw5a  
OK, so far, so good. Now, work on the -1 by adding a 0 as -1+1.
rw5aa
a = 2 and b = 4

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".