|
An exponential equation is one in which a variable occurs in the exponent.
|
 Solution Method 1: Using a Common Base Solution Method 1: Using a Common Base |
An exponential equation in which each side can be expressed in terms of
the same base can be solved using this property:
if bx = by, then x = y (where b > 0 and b ≠1).
If the bases are the same, set the exponents equal. |

| |
Solve for x: |
Answer |
1. |
|
Since the bases are the same, set the exponents equal to one another and solve for x:
3x - 2 = 2x + 1
x = 3 |
2. |
|
27 can be expressed as a power of 3:
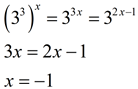
|
3. |
|
Both 8 and 32 can be expressed as powers of 2:
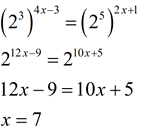 |
4. |
|
Both 125 and 1/25 can be expressed as powers of 5: 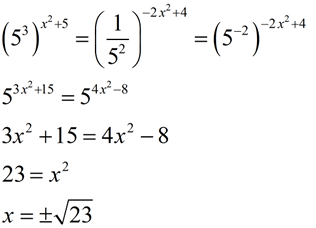
|
| Unfortunately, not all exponential equations can be expressed in terms of a common base. For these equations, logarithms are used to arrive at a solution. (You may solve using common log or natural ln, but when working with e, use ln.) |
Remember:
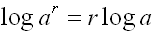
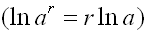 |
|
 Solution Method 2: Using logs Solution Method 2: Using logs |
To solve most exponential equations:
1. Isolate the exponential expression.
2. Take log or ln of both sides, to set up the inverse relationship between exponentials and logarithms.
3. Use this inverse relationship:
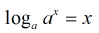 (where a > 0, a ≠1, and logaax is defined) (where a > 0, a ≠1, and logaax is defined).
4. Solve for the variable.
|
|
Things to remember
about logs:
|
|
 Grab your calculator! Grab your calculator!
| |
Solve for x,
to nearest thousandth: |
Answer |
1. |
5x = 7
* Can you see how trying to get a common base for 5 and 7 would be an extremely difficult task? The log method will save us a good deal of aggravation on this problem.
Also notice that the solution can be found using either log or log5. |
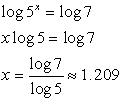 OR
OR
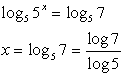 |
• Take the log of both sides.
• Apply the log power rule.
• Solve for x.
• Estimate answer from calculator
• log base 5 can also be used as a solution method.
• notice how the log5 of 5x is really composition of inverses and yields x.
• Notice the change of base formula used at the end for the calculator.
|
|
2. |
15 = 32x+1 |
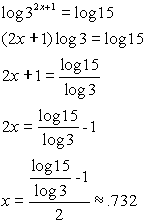 |
OR |
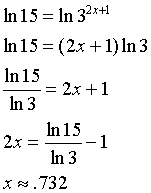 |
|
3. |
ex = 43 |
Since the natural log is the inverse of the natural exponential function, use ln to quickly solve this problem.
ln ex = ln 43
x = ln 43 ≈ 3.761
|
4. |
|
|
• First, get rid of the coefficient of the exponential term (divide by 150).
• Now, proceed using ln to quickly solve.
• Do not round too quickly. Be sure to carry enough decimal values to allow you to round to thousandths (in this case) for the final answer. |
|
5. |
|
|
• Isolate the exponential
• Take the log of both sides
• Apply the log property
• Divide by log 4
• Estimate using calculator |
|
6. |
|
|
• First, divide by the coefficient to isolate the exponential
• Take the log of both sides
• Apply the log rule
• Divide by log 2
• Estimate answer |
|
7. |
|
|
• Isolate the exponential
• Divide each side by the coefficient of 2
• Take ln of both sides
• Remember that ln x and ex are inverse functions. |
|
8. |
|
This question requires some additional thinking. Because of the differing powers of e, our previous methods will not be of much help. We will need a different strategy for this problem.
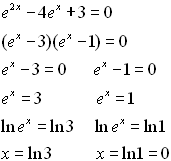 |
• Remember that ex • ex = e2x
• This problem is really
x2 - 4x + 3 = 0 where x = ex
• Factor
• Both solutions are answers. |
|
|
For help with exponential equations on
your calculator,
click here.
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|