When the imaginary unit, i, is raised to increasingly higher powers,
a cyclic (repetitive) pattern emerges.
Remember that i 2 = -1. |
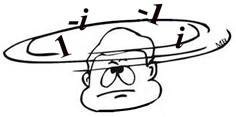 |
Repeating Pattern of Powers of i : |
i0 = 1 |
i4 = i3 • i = (-i) • i = -i2 = 1 |
i8 = i 4• i4 = 1 • 1 = 1 |
i1 = i |
i5 = i 4• i = 1 • (i) = i |
i9 = i 4• i 4• i = 1 • 1• i = i |
i2 = -1 |
i6 = i 4• i2 = 1 • (-1) = -1 |
i10 = (i 4)2 • i2 = 1 • (-1) = -1 |
i3 = i2 • i = (-1) • i = -i |
i7 = i 4• i3 = 1 • (-i) = -i |
i11 = (i 4)2 • i3 = 1 • (-i) = -i |
The powers of i repeat in a definite pattern: (i, -1, -i, 1)
Powers of i |
i -2 |
i -1 |
i 0 |
i 1 |
i 2 |
i 3 |
i 4 |
i 5 |
i 6 |
i 7 |
i 8 |
Simplified Form |
-1 |
-i |
1 |
i |
-1 |
-i |
1 |
i |
-1 |
-i |
1 |
Notice how the pattern continues even as we move to the left of i 1 in the chart.
This gives us an understanding of how to address statements such as:
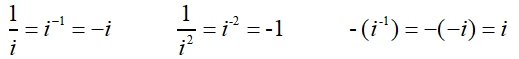
Cyclic Nature of i
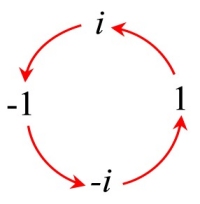
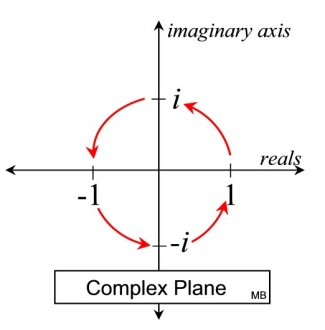
When viewed in the complex plane, it can be seen that these values follow a pattern that coincides with the numbering on the coordinate axes.
|
 |
Simplifying powers of i:
You will need to remember (or establish) the powers of 1 through 4 of i to obtain one cycle of the pattern. From that list of values, you can easily determine any other positive integer powers of i.
Method 1: When the exponent is greater than or equal to 5, use the fact that i 4 = 1
and the rules for working with exponents
to simplify higher powers of i.
Break the power down to show the factors of four.
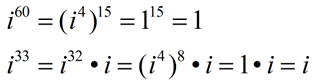 |
 When raising i to any positive integer power,
the answer is always
i, -1, -i or 1. |
|
Another way to look at the simplification:
Method 2: Divide the exponent by 4:
• if the remainder is 0, the answer is 1 (i0).
• if the remainder is 1, the answer is i (i1).
• if the remainder is 2, the answer is -1 (i2).
• if the remainder is 3, the answer is -i (i3). |
|

|