In Algebra 1, we stumbled upon the issue of negative numbers appearing under a radical when we were working with quadratic equations and the quadratic formula. At that time, we recognized that such a situation would lead to a solution that was not a real number.
In Algebra 2, we are ready to extend our investigation of complex numbers in the area of quadratics. On this page, let's take a quick computational look at quadratics and complex numbers, with a more in-depth discussion under the topic of Quadratics.
Quadratic Equations and Complex Numbers |
Solve the equation: x2 + 4 = 0
While the solution is not a Real number, there is a solution that is a complex number.
Solve the equation: x2 + 24 = 0
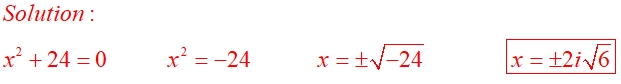
When a complex solution contains a radical symbol, it is customary to place the "i" in front of the radical symbol, so it does not appear that the "i" might be "under" the radical symbol.
Solve the equation: 3x2 - 12 = -42
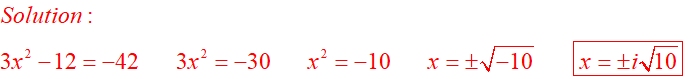
Solve using the quadratic formula: x2 - 6x + 13 = 0
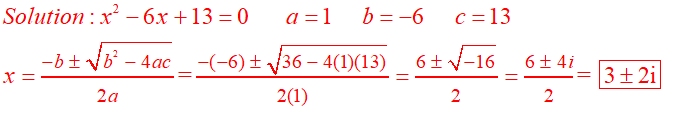
Solve using the quadratic formula: x2 - 3x + 10 = 0
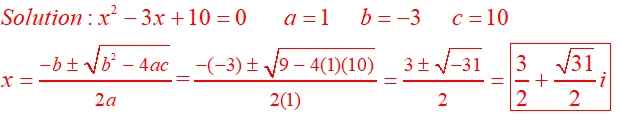
If a problem asks for the solution in "a + bi" form, you must separate the answer into two fractional parts.
Leaving the final answer over one denominator would not be answering the question, If the problem does not specify a form for the answer, then an equivalent solution may be acceptable. When working with complex numbers, an "i" is expected in the solution, when needed.
