| Does anyone ever really use complex numbers? |
Complex numbers offer a means of finding the roots of polynomials, and polynomials are used as theoretical models in a variety of fields. Consequently, complex numbers enjoy prominence in several specialized areas, including general engineering, electrical engineering and quantum mechanics. Such topics as electrical current, the design of dynamos and electric motors, liquid flow in relation to obstacles, wavelength, analysis of stress on beams, the study of resonance of structures, the movement of shock absorbers in cars, and the manipulation of large matrices used in modeling utilize complex numbers.
For example, electrical engineers discovered, when studying alternating current (AC) circuits, that the quantities of voltage, current and resistance, called impedance in AC, were not the familiar one-dimensional scalar quantities (regular numbers) that are used when measuring direct current (DC) circuits. These quantities which now alternate in direction and amplitude possess other dimensions (frequency and phase shift) that must be taken into account. In order to represent the two dimensions of frequency and phase shift, complex numbers were used with j representing the imaginary unit i to avoid confusion with the symbol for electric current which is I.
The form a + jb is used with the formula E = I • Z, where E is voltage (volts), I is current (amps) and Z is impedance (ohms).
AC circuit components such as resistors, inductors and capacitors all oppose the flow of current. The opposition to current is referred to as resistance for resistors and reactance for inductors and capacitors. The total opposition to current flow in a circuit is called impedance, Z, measured in ohms, 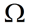 . .
(Note in the table below that impedance referred to as resistance is represented with a Real Number while impedance referred to as reactance is represented with an Imaginary Number. Impedance from Inductors is positive, and from Capacitors is negative.)
Circuit Component |
Symbol |
Impedance (Z) |
Resistor |
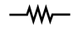 (5 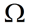 ) ) |
Z = 5 |
Inductor |
 (6 (6 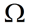 ) ) |
Z = 6i |
Capacitor |
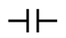 (7 (7 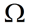 ) ) |
Z = -7i |

In a series circuit, the impedance is the sum of the impedances for the individual components.
In a parallel circuit, there is more than one pathway through which the current can flow. To find the total impedance, ZT, first calculate the impedances Z1 and Z2 of the pathways separately, by treating each pathway as a series circuit.
Then apply the formula 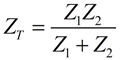 . .
You will put this information to use on the Complex Numbers and Electricity Practice page.
|