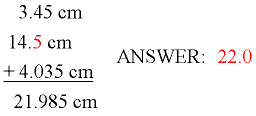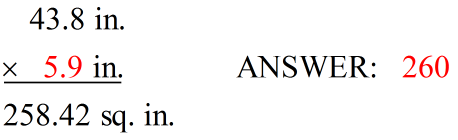|
 |
The concept of significant figures (or digits) is a convention for expressing the accuracy of a measurement. |
|
When working with real-world data, it is crucial that every measured value be as accurate as possible. Attempts must be made to minimize uncertainty when expressing measurements. To accomplish this task, certain rules are followed by scientists and engineers to maintain a level of accuracy and to communicate this level with other individuals.
 The Rules for Significant Figures:
1) All nonzero numbers (1,2,3,4,5,6,7,8,9) are significant.
56 has 2 significant figures.
3,456,789 has 7 significant figures.
2) All zeros between non-zero numbers are significant.
306 has 3 significant figures.
10.05 has 4 significant figures.
3) Leading zeros are not significant.
0.025 has 2 significant figures.
4) Trailing zeros to the right of the decimal are significant.
300.0 has 4 significant figures.
24.300 has 5 significant figures.
5) Trailing zeros in a whole number with a decimal point are significant.
1200. has 4 significant figures.
1200 has 2 significant figures.
6) Trailing zeros in a whole number without a decimal are NOT significant.
1200. has 4 significant figures.
1200 has 2 significant figures.
Confused?? |
5000 ft. |
This number is read as being accurate to the thousands place. Without a decimal point, we don't know if this number was exactly 5000 feet, or if it was rounded up or rounded down to this value (or to which place-value it was rounded - ones, tens, hundreds, etc.).
It has 1 significant figure.
|
5000. ft. |
The decimal point indicates that this number is accurate to the units place. The measurement was 5000 feet to the nearest foot.
It has 4 significant figures. |
5000.0 ft. |
The decimal point indicates that this number is accurate to the tenths place. The measurement was 5000 feet to the nearest tenth of a foot.
It has 5 significant figures. |
|
 |
Arithmetic with Significant Figures:
*** You cannot improve the accuracy by doing arithmetic with measurements.
ADDITION/SUBTRACTION:
Add (or subtract) the numbers and round the result to the same decimal place as the least-accurate number.
|
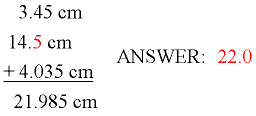The least-accurate number in this sum is 14.5, showing one decimal place. The answer must be rounded to one decimal place.
|
MULTIPLYING/DIVIDING:
Multiply (or divide) the numbers and round the answer to the same number of significant digits as the least-accurate number.
|
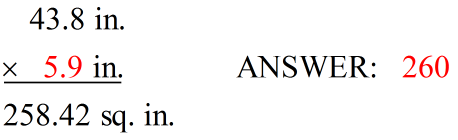
The least-accurate number in this product is 5.9 which has 2 significant digits. The answer must be rounded to 2 significant digits. |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
