|
In addition to solving systems of equations algebraically, you can also solve them graphically. A graphic solution can be done by hand (on graph paper), or with the use of a graphing calculator.
 Graphical Method - on graph paper |
Graphing a system of linear equations is as simple as graphing two straight lines. When the lines are graphed, the solution will be the (x,y) ordered pair where the two lines intersect (cross).
|
* Before you begin, rearrange the equations so they will read "y =". This process will make it easier to read the slope and y-intercept, for the slope-intercept method of graphing.
|
|
Solve this system of equations graphically and check your solution:
(easy one)
|
y = 2x + 1 and y = -x + 7 |
1. The equations in this example are already set equal to "y". Identify the slope and y-intercept in each equation. Remember: y = mx + b, where m = slope and b = y-intercept. |
y = 2x + 1
slope = 2
y-intercept = 1
|
y = -x + 7
slope = -1
y-intercept = 7 |
2. Graph the lines.
This example used the slope-intercept method of graphing straight lines.
The b-value tells you where the line crosses the y-axis.
The slope, m, tells you the rise over the run.
If you need help graphing lines, see
Graphing Linear Equations. Find the intersection point (where the lines cross).
These lines cross at the point (2,5).
This means the solution to this system is:
Solution: x = 2 and y = 5. |
|
3. CHECK: Substitute x = 2 and y = 5 into BOTH of the original equations. If your solutions are correct, both equations will be true! |
y = 2x + 1
5 = 2(2) + 1
5 = 5 (check)
|
y = -x + 7
5 = -(2) + 7
5 = 5 (check)
|
 Two special cases!
1. Parallel Lines:
If the two linear equations have the same slope (and different y-intercepts), the lines will be parallel. Since parallel lines never intersect, a system composed of two parallel lines will have NO solution (no intersection of the lines.)
Solve system: y = 2x + 4 and y = 2x - 2
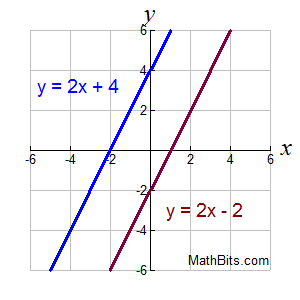
Solution: No solution
|
2. Same Line:
If the two linear equations have the same slope (and the SAME y-intercept), the equations represent the same line. Since a line intersects with itself everywhere, there will be an infinite number of solutions (intersecting everywhere.)
Solve system: y = -2x + 1 and 2x + y = 1
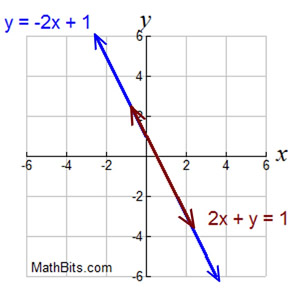
Solution: Infinite number of solutions |
|
|
Solve this system of equations graphically and check your solution:
(harder one)
|
x = y + 1 and 2x + y = -7
|
1. Set the equations equal to y to make graphing easier. |
|
2. Identify the slope and y-intercept in each equation.
|
y = x - 1
slope = 1
y-intercept = -1 |
y = -2x - 7
slope = -2
y-intercept = -7 |
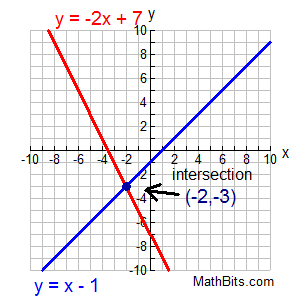
3. Graph the lines.
Find the intersection point (where the lines cross).
These lines cross at the point (-2,-3).
This means the solution to this system is:
x = -2 and y = -3.
|
 |
4. CHECK: Substitute x = -2 and y = -3 into BOTH of the original equations. If your solutions are correct, both equations will be true! |
x = y + 1
-2 = -3 + 1
-2 = -2 (check)
|
2x + y = -7
2(-2) + (-3) = -7
-4 + (-3) = -7
-7 = -7 (check) |
The graphing method on graph paper can be useful when the intersection point happens to have integer coordinates (as seen in the example above). It becomes less helpful, however, when the coordinates are not integers. If it appears that the intersection point does not lie on the intersection of the grids of the graph paper, try an algebraic solution method or grab your graphing calculator.
| Graphical Method - graphing calculator |
|
When using the graphing calculator, you will still need to set the equations equal to y before you begin.
Follow the link at the right to see how to use your graphing calculator.
|
|
|
|
For calculator help with systems of equations
click here. |
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
