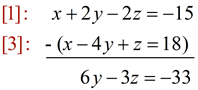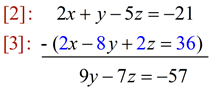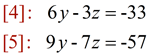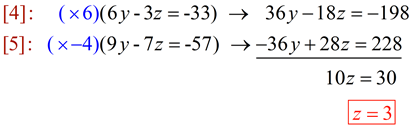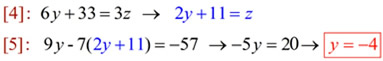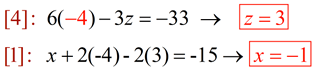We will examine how the Elimination Method and the Substitution Method used to solve 2 x 2 linear systems can be applied to 3 x 3 linear systems. All of the variables will be of degree 1 (linear system). x + 2y - 2z = -15 2x + y - 5z = -21 x - 4y + z = 18 Algebraic Solution by Elimination

The Elimination Method used with 2 x 2 linear systems will be put to more "active" use
in a 3 x 3 linear system. The goal will be to eliminate a variable, thus creating a more easily solved 2 x 2 linear system.

Steps to Solving by Elimination: This process will be similar to that used for 2 x 2 systems, only repeated more times.	[1]:     x + 2y - 2z = -15 [2]:    2x + y - 5z = -21 [3]:      x - 4y + z = 18	This method works well!
1. Start with any two equations to eliminate a variable. Choose the easiest variable to eliminate. Then choose a different pair of equations and eliminate the same variable. You will be left with a 2 x 2 system. Eliminate the same variable from two pairs: To eliminate "x", subtract [3] from [1] and get: 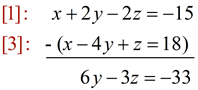           To eliminate "x" again, multiply [3] by 2, subtract from [2] and get:
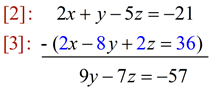2. Now, solve the new 2 x 2 system by elimination. Set up the two new equations as a 2 x 2 system and solve: Set up the new 2x2 system: 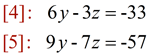To eliminate "y", multiply [4] by 6, [5] by -4, and add: 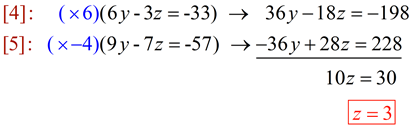Now that we have z = 3, substitute z back into [4] or [5] to find the value of y:
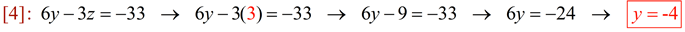3. Substitute the solutions for z and y back into [1], [2] or [3] to find the value of x: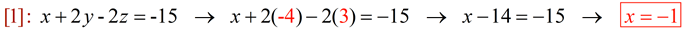
4. ANSWER:      x = -1; y = -4; z = 3      or      {-1, -4, 3}

This method shows "one" way to arrive at the answers. Other equations could have been chosen throughout the process.

Algebraic Solution by Substitution

The Substitution Method we used with 2 x 2 linear systems will require more "repeated" use when working with a 3 x 3 linear system. The goal will to solve for one variable and reduce the system by plugging into the other equations. This process is repeated until one equation (one variable) is left. Back-substitution is then used to determine the remaining unknown variables.

Steps to Solving by Substitution: This process will be similar to that used for 2x2 systems, but will require more simplification.	[1]:     x + 2y - 2z = -15 [2]:    2x + y - 5z = -21 [3]:      x - 4y + z = 18	This method works well!
Solve for one variable: 1. Start with any of the equations. Pick any variable in the equation and solve for it. We will pick equation [3], and solve for x.    [3]:     x - 4y + z = 18               x = 18 + 4y - z
Plug into other two equations: 2. Now, substitute this value for x into the other two equations, [1] and [2], and simplify. Substitute into [1]: [1]:    x + 2y - 2z = -15           (18 + 4y - z) + 2y - 2z = -15            6y - 3z = -33 Substitute into [2]: [2]:   2x + y - 5z = -21          2 (18 + 4y - z) + y - 5z = -21          9y - 7z = -57
Now, use substitution method for new 2 x 2 system: 3. You now have a system with two equations and two unknowns, y and z. You could solve these two equations by any method, but we will continue with the substitution method. Set up the new 2 x 2 system: 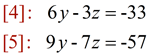Solve [4] for z, then plug into [5] for z, and solve: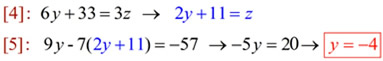
4. Substitute y = -4 into [4] and solve for z. Then plug both values into [1], [2] or [3] and solve for the variable x.
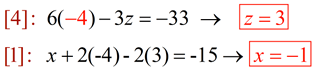5. ANSWER:      x = -1; y = -4; z = 3      or      {-1, -4, 3}

This method shows "one" way to arrive at the answers. Other equations could have been chosen throughout the process.