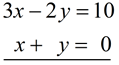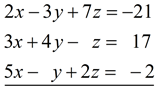|
When working with 2 x 2 linear systems,
you are working with lines.
Two lines can intersect in a point, can be parallel to
one another, or can be the same line.
When working with 3 x 3 linear systems,
you are working with planes.
Three planes
can intersect in a point, can intersect in a line,
can not intersect at all, or can all be the same plane.
All of which are difficult to display on paper. |
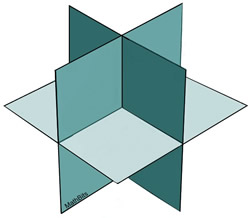 When there is one point common to all
three planes, there will be a solution (an
ordered triple) to the 3x3 system.
|
The goal to solving a 3 x 3 system of linear equations is to find a value for each of the variables that will satisfy all three of the equations, making each equation true. |
LINEAR SYSTEMS: Generally refer to 2 x 2 or 3 x 3 linear systems.
A 2 x 2 linear system deals with two variables, such as x and y.
A 3 x 3 linear system deals with three variables, such as x, y and z.
2 x 2 System of Linear Equations
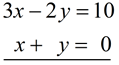
Solution: (x, y) = (2,-2)
|
3 x 3 System of Linear Equations
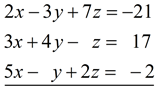
Solution: (x, y, z) = (1, 3, -2) |
We found, when solving 2 x 2 systems, that there are three "basic" methods of arriving at the solution: an algebraic solution by substitution, an algebraic solution by elimination, and a graphical solution.
In the following section, we will investigate only the substitution method and the elimination method for solving 3 x 3 linear systems. The graphical approach will be addressed in a future course.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
