When the distributive property is mentioned, we think of:
a ( b + c ) = a • b + a • c = ab + ac
To be more specific, it is officially called:
"the distributive property of multiplication over addition"
Note: you can distribute "over" addition (or subtraction, which is adding a negative),
but you cannot distribute "over" multiplication or division.

There are some really interesting ideas associated
with the distributive property.
Don't
turn the channel just yet.
You may find these ideas interesting and useful!
|
 |
1. |
Distributive Property versus Order of Operations
When dealing with numerical values and simplifying a ( b + c ), the "distributive property" and the "order of operations", are each capable of accomplishing the same task. |
| |
Distributive Property:
3 ( 4 + 2 ) = 3 • 4 + 3 • 2
= 12 + 6
= 18 |
Order of Operations:
3 ( 4 + 2 ) = 3 ( 6 )
= 18
|
2. |
Distributive Property making Multiplication Easier
When working without a calculator, you can use the distributive property to make your multiplication computations easier by breaking a number into components that are easily multiplied in your head. |
| |
Multiply: 6 x 148
Expressing as addition.
6 ( 100 + 40 + 8 )
=
600 + 240 + 48
= 840 + 48
= 888 |
Multiply: 8 x 19
Expressing as subtraction.
8 ( 20 - 1 )
=
160 - 8
= 152
|

3. |
Distributive Property over Multiple Terms
The distributive property works as multiplication over addition "of any number of terms". While we think of a ( b + c ) = a • b + a • c, we could just as easily think of
a ( b + c + d + e) = a • b + a • c + a • d +
a • e (or any number of terms inside the parentheses). |
| |
Distributive Property:
3 ( 4 + 2 + 6 + 1 )
=
3 • 4 + 3 • 2 + 3 • 6 + 3 • 1
= 12 + 6 + 18 + 3
= 39 |
Distributive Property:
2 ( 4n + 1 + 2n + 7 + n)
=
2 • 4n + 2 • 1 + 2 • 2n + 2 • 7 + 2 • n
= 8n + 2 + 4n + 14 + 2n
= 14n + 16
|
| |
This concept is particularly helpful in Algebra as it lets us
distribute a factor over a polynomial. |

4. |
The Distributive Property in Reverse
You can work the distributive property "backward" so that a • b + a • c = a ( b + c ). While is can be referred to as reversing the distributive property, it is actually just pulling out the greatest common factor. |
| |
Distributive Property:
5a + 5b = 5 • a + 5 • b
=
5( a + b )
common factor of 5 |
Distributive Property:
3x2 + 6x + 3 = 3 • x2 + 3 • 2x + 3 • 1
=
3( x2 + 2x + 1 )
common factor of 3
|
5. |
The Distributive Property with Two Sums
When two sums are involved, the distributive property is actually being applied twice. It does not matter which parentheses is first multiplied out. Think of one of the parentheses are being a single entity. |
| |
Distributive Property:
(a + b) • (a - b) = a • (a - b) + b• (a - b)
= a2 - ab + ba - b2
=
a2 - b2 |
Distributive Property:
(a + b) • (a - b) = (a + b) • a - (a + b) • b
= a2 + ba - ab - b2
=
a2 - b2
|
6. |
The Distributive Property in Geometry
When working in geometry, a visual interpretation of the distributive property at work while finding the area of rectangles (using positive numbers for the variables) is shown below.
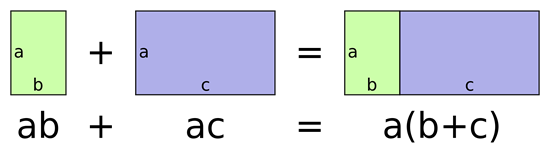 |
|