Rational Expressions
MathBitsNotebook.com

Topical Outline | Algebra 1 Outline | MathBits' Teacher Resources

Terms of Use   Contact Person: Donna Roberts

Rational numbers are denoted by a script Q.

Q stands for "quotient"

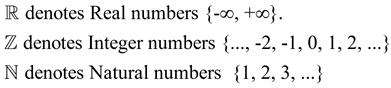
A rational number is a number that can be expressed as a fraction p/q where p and q are integers and q ≠ 0. It is the ratio of two integers.

You are familiar with rational numbers from your work with fractions.

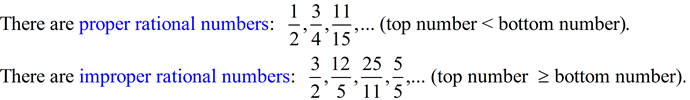
A rational expression is an expression that is the ratio of two polynomials. 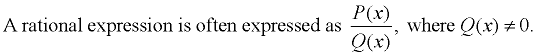(where P(x) and Q(x) are polynomials)

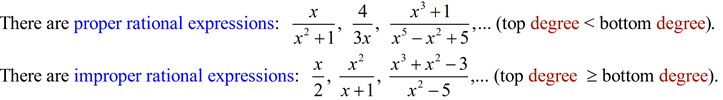
Rational expressions are algebraic fractions in which the numerator is a polynomial and the denominator is also a polynomial (usually different from the numerator). The polynomials used in creating a rational expression may contain one term (monomial), two terms (binomial), three terms (trinomial), and so on.

Rational Expressions (monomial/monomial)	Rational Expression (binomial/binomial)	Rational Expression (binomial/trinomial)

Expressions that are not polynomials cannot be used in the creation of rational expressions.

For example: 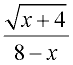is not a rational expression, since 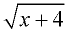is not a polynomial.

Since rational expressions represent division, we must be careful to
avoid division by zero.
If a rational expression has a variable in its denominator, we must ensure that any
value (or values) substituted for that variable will not create a zero denominator.

If it is not obvious which values will cause a division by zero error in a rational expression,
set the denominator equal to zero and solve for the variable.

Rational expression: Could it possibly be undefined? When?		Rational expression: Could it possibly be undefined? When?
	Obviously, when x = 1, the denominator will be zero, making the expression undefined. Domain: All Real numbers but not x = 1.		Set the denominator = 0 and solve. a2 - 4 = 0 a2 = 4
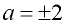For this rational expression, we must limit the x's which may be used, to avoid a division by zero error, and leaving the expression undefined. Notation: 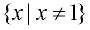read "all x's such that x ≠ 1."		For this rational expression, we must prevent two x-values from being used in the expression. Domain: All Real numbers but not a = 2 nor a = -2.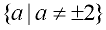
Rational expression: Could it possibly be undefined? When?		Rational expression: Could it possibly be undefined? When?
	Set: 8 - y = 0          8 = y Domain: All Real numbers, except y = 8.		Set: x2 + x - 12 = 0 (x - 3)(x + 4) = 0 x - 3 = 0;     x = 3 x + 4 = 0;    x = -4 Domain: All Real numbers, but not x = 3 and not x = -4.