Summary of Facts on this Page:
• The sum of a rational and an irrational is irrational.
• The product of a non-zero rational and an irrational is irrational. |
 |
|

|
"The sum of a rational number and an irrational number is irrational." |
By definition, an irrational number in decimal form goes on forever without repeating (a non-repeating, non-terminating decimal). By definition, a rational number in decimal form either terminates or repeats. If you add a non-repeating, non-terminating decimal to a terminating decimal, you still have a non-repeating, non-terminating decimal. If you add a non-repeating, non-terminating decimal to a repeating decimal, you will no longer have a repeating decimal.
Examples:
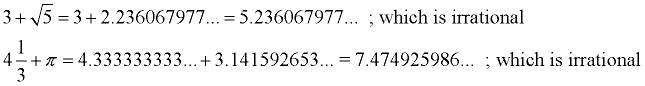
Indirect Proof (Proof by Contradiction):
(Assume the opposite of what you want to prove, and show it leads to a contradiction of a known fact.)



This one is sneaky!!
|
"The product of a "non-zero" rational number and an irrational number is irrational." |
If you multiply any irrational number by any rational number, not zero, the product will be irrational.
A problem
arises if you forget to state "non-zero" rational number. If you multiply any irrational number (or any value) times ZERO, the product is going to be zero. which is a rational number.
 Be careful!!
Be careful!!
If you leave out the "non-zero" statement, the result will change.
"The product of a rational number and an irrational number
is SOMETIMES irrational."
The zero rational number is the only case that causes this problem.
For all other values, the product of a rational and an irrational will be irrational.
Indirect Proof (Proof by Contradiction)
(Assume the opposite of what you want to prove, and show it leads to a contradiction of a known fact.)
