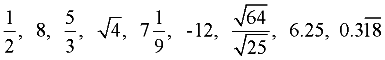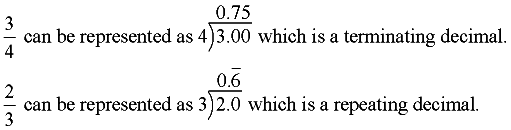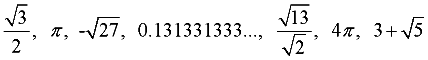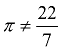|
You may have heard the statement that "mathematics seems to have its own language." In many regards this statement is true. If you look up the definition of the words "rational" and "irrational" from Oxford Languages (the world's most authoritative source on English dictionaries), you will find the most common definitions of these words, followed by their "MATHEMATICS" definitions.
rational: (Oxford Languages' definition)
1. based on reason or logic - "I'm sure there's a perfectly rational explanation."
2. MATHEMATICS: (of a number, quantity, or expression) expressible, or containing quantities that are expressible, as a ratio of integers. When expressed as a decimal, a rational number has a finite or recurring expansion. |
irrational: (Oxford Languages' definition)
1. not logical or reasonable - "irrational feelings of hostility"
2. MATHEMATICS: (of a number, quantity, or expression) not expressible as a ratio of two integers and having an infinite and nonrecurring expansion when expressed as a decimal. Examples of irrational numbers are the number π and the square root of 2. |
So, let's start speaking "mathemaics" and examine rational and irrational numbers.
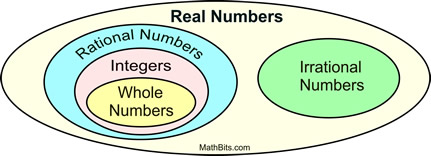
 Rational and irrational numbers belong to the set of Real Numbers.
They are called subsets of the
Real Numbers
|
|
 |
A rational number is a number that can be expressed as a fraction (ratio) in the form 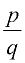 where p and q are integers and q is not zero. |
|
Examples: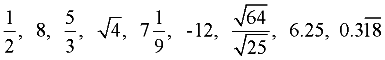 
Remember: The word "rational" contains the word "ratio".
A rational number can be expressed as a ratio (a fraction) of integers.
 When a rational number fraction is divided to form a decimal value,
it becomes a terminating or repeating decimal.
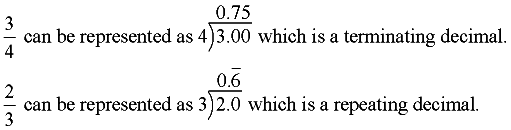
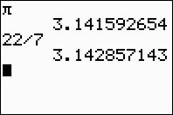
 Some rational fractions may produce a large number of digits in their repeating patterns, which may exceed the size of the viewing screen on a calculator. The fraction 53/83 has a calculator display of 0.6385542169, which shows no repeating pattern, when in reality the pattern will repeat after 41 digits. |
To convert a repeating decimal to a fraction:
Now, that you know how this conversion occurs,
you can simply apply the pattern that can be seen in the conversion steps.
Place the repeating numbers in the pattern in the numerator.
Place that same number of
9's in the denominator.
Reduce the fraction if needed.
|
An irrational number is a number that is NOT rational.
It cannot be expressed as a fraction with integer values in the numerator and denominator. |
|
Examples: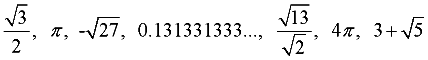 
When an irrational number is expressed in decimal form,
it goes on forever without repeating.
Remember: Like the word "rational", the word "irrational"
also contains the word "ratio".
But the prefix "ir" means "not".
An irrational number can not be expressed as a ratio (a fraction) of integers.
The square root of non-perfect squares are always irrational.
Properties of Rational and Irrational Numbers:
Since rational and irrational numbers are subsets of the real numbers,
they possess all of the properties assigned to the real number system.
|
to represent "pi", these values are only estimates or approximations.
Notice the differences in the decimal representations on the calculator screen at the right. 
