|
The term "quadratic" was briefly introducted in the section on Polynomials.
Quadratics are polynomials of degree two. That is, the largest exponent on the variable is 2.
"Quadratic" expressions also appeared under Factoring,
in the categories of binomials and trinomials.
x2 - 64 = (x + 8)(x - 8) (x + 6)2 = x2 + 12x + 36 x2 - x - 12 = (x - 4)(x + 3)
This Quadratic unit will investigate working with quadratic equations and quadratic graphs.
Quadratic Equations:
|
A quadratic equation is a polynomial equation of degree two,
which can be written in the form ax2 + bx + c = 0, where x is a variable and a, b and c are constants with a ≠ 0. |
|
Consider: If a = 0, there would be no x2 term and the equation would be "linear", not "quadratic".
 Why does "quadratic" refer to equations of degree "two"?
While the prefix "quadri" (in Latin) means four, the word "quadrare" means "to square". Consider, if x is raised to the power of 2, we say x is being "squared".
In early mathematics, quadratic equations were used to model the area of quadrilaterals (and specifically squares). The area of a square, for example, is expressed in "square" units with the length of a side being "squared" (raised to a power of 2). Thus the connection between "quadratic", "squaring" and "two". The power of two is referred to as "squaring", and equations with a power of two are called quadratic equations.
|
 |
Solving quadratic equations:
Solving a quadratic equation can range from being a simple task, to being a challenge. In this quadratic section, we will be building our arsenal of strategies for solving quadratic equations. |
Quadratic Equation Strategies:
|
|
We will be examining each of the strategies for solving quadratic equations
shown in the table above.
Quadratic Functions:
 |
A quadratic function is a second degree polynomial represented as
y = ax2 + bx + c or f (x) = ax2 + bx + c
where a, b and c are constants with a ≠ 0. |
|
Let's take a quick look at the graph of a quadratic function.
We will investigate graphing more thoroughly in upcoming lessons.
Example:
Graph the quadratic function y = x2 - 4x on the interval -1 < x < 5.
| x |
x2 - 4x |
y |
| -1 |
(-1)2 - 4(-1) |
5 |
| 0 |
(0)2 - 4(0) |
0 |
| 1 |
(1)2 - 4(1) |
-3 |
| 2 |
(2)2 - 4(2) |
-4 |
| 3 |
(3)2 - 4(3) |
-3 |
| 4 |
(4)2 - 4(4) |
0 |
| 5 |
(5)2 - 4(5) |
5 |
|
Plot the
points generated in the chart. Draw a
smooth curve through the points.
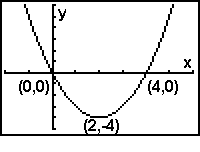
The points where the graph crosses the
x-axis are the zeros ( or roots of the quadratic equation
0 = x2 - 4x).
This parabola crosses the x-axis
at (0,0) and (4,0).
|
|
Notice the characteristics of this graph:
• the graph sort of takes the shape of a capital letter U (but not quite).
• the graph "turns", changing from decreasing to increasing.
• the graph has y-values that repeat along the graph, such as (1,-3) and (3,-3). This did not happen with the graph of a straight line.
• the locations where the graph crosses the x-axis correspond to the solutions to the quadratic equation associated with the function.
y = x2 - 4x quadratic function
0 = x2 - 4x associated quadratic equation
0 = x(x - 4) factor
x = 0; x - 4 = 0 set factors = 0
x = 0, x = 4 solve for x
(0,0) and (4,0) graph crosses x-axis |
The graph of a quadratic function is called a parabola.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
