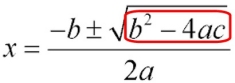In Algebra 1, the discriminant is used to verify that there are no Real solutions or roots for quadratic equations.
When solving a quadratic equation, we are searching for the two solutions that will make the equation true. We have encounter situations where there appeared to be only one solution (a repeated root), or even situations where there were no Real number solutions to the equations.
 Is there a way to "know" whether there will be 0, 1 or 2 solutions to a quadratic equation?
Is there a way to "know" whether there will be 0, 1 or 2 solutions to a quadratic equation?
The answer is "yes", and is connected to the quadratic formula.
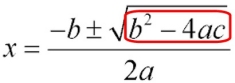
The discriminant is the portion "under" the square root symbol
in the Quadratic Formula: |
The value under the radical (square root) portion of the quadratic formula indicates the number of solutions for that specific quadratic equation. That value is "b2 - 4ac".
b2 - 4ac is called the discriminant. |
|
| Note: The discriminant, b2 - 4ac, does NOT tell you what the solution(s) to the quadratic equation will be. It simply tells you "how many" real solutions there will be.
If the discriminant is a positive number = 2 Real roots.
If the discriminant is zero = 1 Real root. (repeated roots)
If the discriminant is a negative number = 0 Real roots. |
DISCRIMINANT: Its purpose is to tell "how many roots", and "what type of roots". |
POSITIVE
b2 - 4ac > 0 |
ZERO
b2 - 4ac = 0 |
NEGATIVE
b2 - 4ac < 0 |
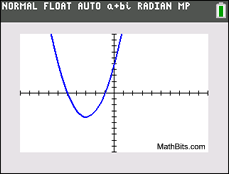
x2 + 6 x + 5 = 0
discriminant:
b2 - 4ac = 62 - 4(1)(5)
= 16 (positive)
There are two real roots.
There are two x-intercepts.
 If the discriminant is a perfect square, the two roots are rational numbers. If the discriminant is not a perfect square, the two roots are irrational numbers containing a radical.
If the discriminant is a perfect square, the two roots are rational numbers. If the discriminant is not a perfect square, the two roots are irrational numbers containing a radical.
x2 + 6x + 5 = (x + 1)(x + 5) = 0
Roots: x = -1, x = -5 |
x2 - 2x+ 1 = 0
discriminant:
b2 - 4ac = (-2)2-4(1)(1)
= 0 (zero)
There is one real root.
There is one x-intercept.
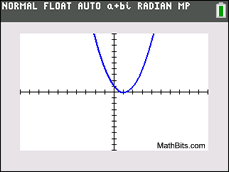
(The root is repeated.)
x2 - 2x+ 1 = (x - 1)2
= (x - 1)(x - 1) = 0
Repeated root: x = 1
|
x2 - 3x + 10 = 0
discriminant:
b2 - 4ac = (-3)2-4(1)(10)
= -31 (negative)
There are NO real roots.
There are no x-intercepts.
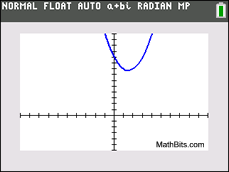 In this situation, there will be two "complex" roots because there will be a negative number under the square root. The answers involve the imaginary number, i.
In this situation, there will be two "complex" roots because there will be a negative number under the square root. The answers involve the imaginary number, i.
|