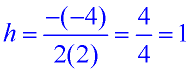|
| FYI: Different textbooks have different interpretations of the reference "standard form" of a quadratic function. Some say
f (x) = ax2 + bx + c is "standard form", while others say that f (x) = a(x - h)2 + k is "standard form". To avoid confusion, this site will not refer to either as "standard form", but will reference f (x) = a(x - h)2 + k as "vertex form" and will reference f (x) = ax2 + bx + c by its full statement. |
 |
The vertex form of a quadratic function is given by
f (x) = a(x - h)2 + k,
where (h, k) is the vertex of the parabola.
|
Remember: the "vertex? is the "turning point".
When written in "vertex form":
• (h, k) is the vertex of the parabola, and x = h is the axis of symmetry.
•
the h represents a horizontal shift (how far left, or right, the graph has shifted from x = 0).
• the k represents a vertical shift (how far up, or down, the graph has shifted from y = 0).
• notice that the h value is subtracted in this form, and that the k value is added.
If the equation is y = 2(x - 1)2 + 5, the value of h is 1, and k is 5.
If the equation is y = 3(x + 4)2 - 6, the value of h is -4, and k is -6.

 To Convert from f (x) = ax2 + bx + c Form to Vertex Form: To Convert from f (x) = ax2 + bx + c Form to Vertex Form:
Method 1: Completing the Square
To convert a quadratic from y = ax2 + bx + c form to vertex form, y = a(x - h)2+ k, you use the process of completing the square. Let's see an example.
 Convert y = 2x2 - 4x + 5 into vertex form, and state the vertex. Convert y = 2x2 - 4x + 5 into vertex form, and state the vertex.
Equation in y = ax2 + bx + c form. |
y = 2x2 - 4x + 5 |
Since we will be "completing the square" we will isolate the x2 and x terms ... so move the + 5 to the other side of the equal sign. |
y - 5 = 2x2 - 4x |
We need a leading coefficient of 1 for completing the square ... so factor out the current leading coefficient of 2. |
y - 5 = 2(x2 - 2x) |
Get ready to create a perfect square trinomial. BUT be careful!! In previous completing the square problems with a leading coefficient not 1, our equations were set equal to 0. Now, we have to deal with an additional variable, "y" ... so we cannot "get rid of " the factored 2. When we add a box to both sides, the box will be multiplied by 2 on both sides of the equal sign. |
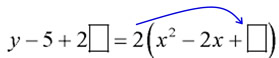
|
Find the perfect square trinomial. Take half of the coefficient of the x-term inside the parentheses, square it, and place it in the box. |
|
Simplify and convert the right side to a squared expression. |
y - 3 = 2(x - 1)2 |
Isolate the y-term ... so move the -3 to the other side of the equal sign. |
y = 2(x - 1)2 + 3 |
In some cases, you may need to transform the equation into the "exact" vertex form of
y = a(x - h)2 + k, showing a "subtraction" sign in the parentheses before the h term, and the "addition" of the k term. (This was not needed in this problem.) |
y = 2(x - 1)2 + 3
Vertex form of the equation.
Vertex = (h, k) = (1, 3)
(The vertex of this graph will be moved one unit to the right and three units up from (0,0), the vertex of its parent y = x2.)
|
Here's a sneaky, quick tidbit:
 |
When working with the vertex form of a quadratic function,
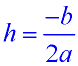 and 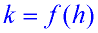 .
The " a" and " b" referenced here refer to f ( x) = ax2 + bx + c. |
Method 2: Using the "sneaky tidbit", seen above, to convert to vertex form:
y = ax2 + bx + c form of the equation. |
y = 2x2 - 4x + 5 |
Find the vertex, (h, k).
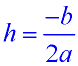 and 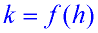 .
[ f ( h) means to plug your answer for h into the original equation for x.]
|
a = 2 and b = -4
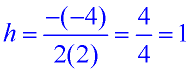
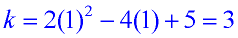
Vertex: (1,3)
|
Write the vertex form.
y = a(x - h)2 + k |
y = 2(x - 1)2 + 3 |

 To Convert from Vertex Form to y = ax2 + bx + c Form: To Convert from Vertex Form to y = ax2 + bx + c Form:
Simply multiply out and combine like terms: |
y = 2(x - 1)2 + 3
y = 2(x2 - 2x + 1) + 3
y = 2x2 - 4x + 2 + 3
y = 2x2 - 4x + 5
|

 Graphing a Quadratic Function in Vertex Form: Graphing a Quadratic Function in Vertex Form:
1. Start with the function in vertex form:
y = a(x - h)2 + k
|
y = 3(x - 2)2 - 4
|
2. Pull out the values for h and k.
If necessary, rewrite the function so you can clearly see the h and k values.
(h, k) is the vertex of the parabola.
Plot the vertex.
|
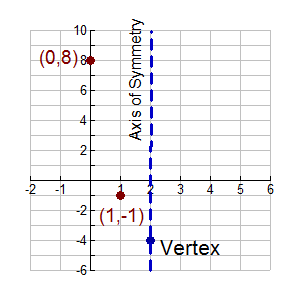
y = 3(x - 2)2 + (-4)
h = 2; k = -4
Vertex: (2, -4)
|
3. The line x = h is the axis of symmetry.
Draw the axis of symmetry.
|
x = 2 is the axis of symmetry |
4. Find two or three points on one side of the axis of symmetry, by substituting your chosen x-values into the equation.
For this problem, we chose (to the left of the axis of symmetry):
x = 1; y = 3(1 - 2)2 - 4 = -1
x = 0; y = 3(0 - 2)2 - 4 = 8
Plot (1, -1) and (0,8) |
|
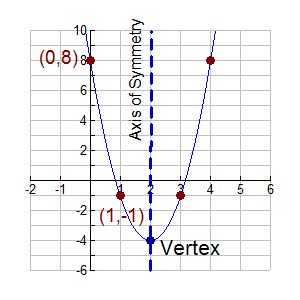
5. Plot the mirror images of these points across the axis of symmetry, or plot new points on the right side.
Draw the parabola.
Remember, when drawing the parabola to avoid "connecting the dots" with straight line segments. A parabola is curved, not straight, as its slope is not constant. |
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|

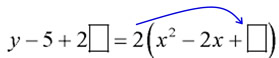

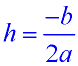 and
and