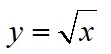|
In this lesson, we will take an introductory look at square root functions and cube roots functions and their relationships to quadratic functions and cubic functions respectively.
You may remember that squaring and square rooting are "inverse" operations.
One operation undoes the other operation.
If we square 4 we get 16. If we take the square root of 16, we are back to 4.
The square root "undoes" what the squaring did (and vice versa).
 Remember, when working with square roots,
the value under the square root symbol cannot be negative. |
Remember: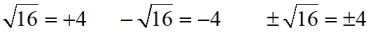 
If no sign is shown in front of the square root symbol, it is assumed to be +,
and is called the Principal Square Root.
|
A square root function is a function of the form f(x) = √x .
It is the inverse of the square function (quadratic) f(x) = x².
The square and square root are inverse functions and are symmetric about the identity line y = x for the domain [0,∞). The range will be [0,
∞). |
Let's compare the basic (parent) quadratic function to the basic (parent) square root function.
Quadratic Function
 |
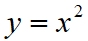Square Root Function
 |
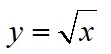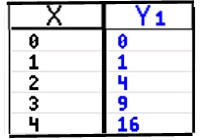
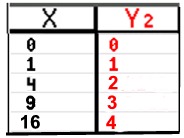
| Let's start this investigation with a few select values in a Table of values: |
|
|
Notice that the columns of values have "switched places" between the quadratic function (on the left), and the square root function (on the right). The x and y values have "swapped" positions. Remember, "squaring" and "square rooting" are inverse operations. |
|
 |
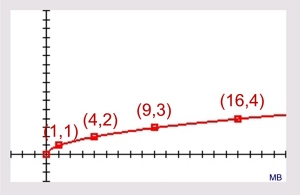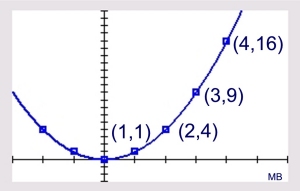
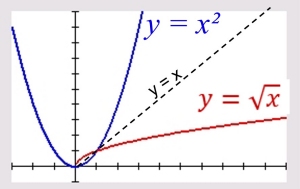
If we put the two functions on the same graph we can see how they are relating to one another.
1. since the square root function is limited to only values greater than or equal to 0 for x, we will need to look only in that domain, [0,∞).
2. we can notice how the shapes of the two graphs are similar. For x > 0, the graphs are reflections over the line y = x. |
 |
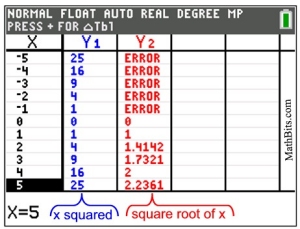
When we graph both functions, and examine the graphs in a table, we can see that the calculator understands that the square root function cannot deal with x-values that are negative (x < 0).
An ERROR message appears to indicate that the square root of a negative value will not be a real number (it will be an imaginary number). |
 |
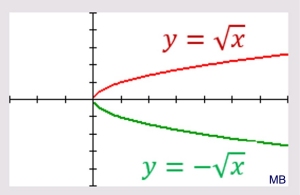
If you thought that the square root graph looks like "half of a parabola", you would be correct.
If we reflect the square root function over the x-axis, the two graphs put together form a parabola. The equation of this sideways parabola will be y2 = x. |
 |
 Cube root functions are not included in the NY NGMS.
Just as the square root function was the inverse of the square (quadratic) function,
so is the cube root function the inverse of the cubic function.
|
A cube root function:  .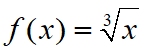
It is the inverse of the cubic function f(x) = x 3.
The cubic and cube root are inverse functions.
The domain will be all real numbers. |
Let's compare the basic (parent) cubic function to the basic (parent) cube root function.
Cubic Function
f (x) = x3 |
Cube Root Function
|
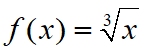| Unlike the square root function, the domain of the cube root function is not limited. |
|
|
Notice that the columns of values have "switched places" between the cubic function (on the left), and the cube root function (on the right). The x and y values have "swapped" positions. Remember, "cubing" and "cube rooting" are inverse operations. |
 |
|
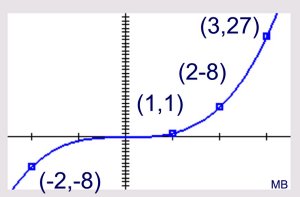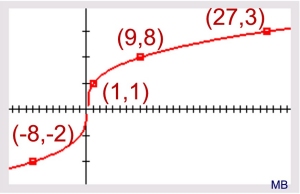
If we put the two functions on the same graph we can see how they are relating to one another.
1. unlike the square root functions, the cube root function has no limitations on the domain.
2. but, in the same fashion as the square root function, the cube root function is the inverse of the cubic function. The cube root function and its inverse (the cubic function) are reflections of one another over the line y = x. |
 |
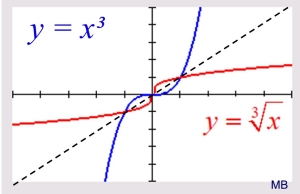NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
