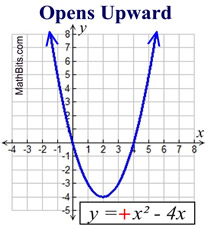
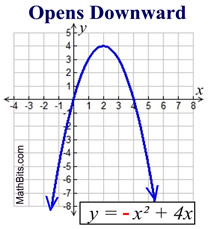
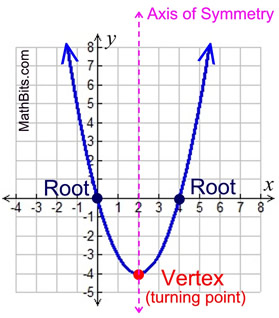
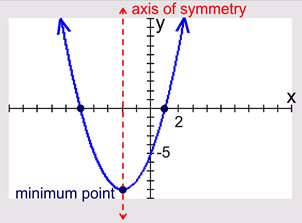
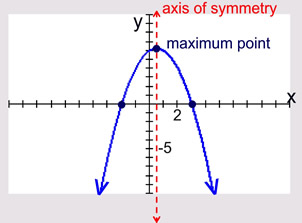
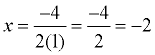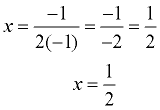definition
The graphs of quadratic functions,  f (x) = ax2 + bx + c,
are called parabolas.

button Shape of the Graph:
graphup graphup
Parabolas have a shape that resembles (but is not quite the same as) the letter U.

Parabolas may open upward or downward.

If the sign of the leading coefficient, a, is positive (a > 0), the parabola opens upward.

If the sign of the leading coefficient, a, is negative (a < 0), the parabola opens downward.

 

button Parts of the Graph:
graphvocab
The bottom (or top) of the U is called the vertex, or the turning point. The vertex of a parabola opening upward is also called the minimum point. The vertex of a parabola opening downward is also called the maximum point.

The x-intercepts are called the roots, or the zeros. To find the x-intercepts, set ax2 + bx + c = 0.

The ends of the graph continue to positive infinity (or negative infinity) unless the domain (the x's to be graphed) is otherwise specified.

 

button Axis of Symmetry:
The parabola is symmetric (a mirror image) about a vertical line drawn through its vertex (turning point). This line is called the axis of symmetry. The equation for the axis of symmetry is 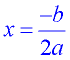symmetryeq.
Parabola:   y = x2 + 4x - 5

Axis of symmetry: symmetryeq
quadsypiceq1
x = -2

quadsmpic1

Determine the coordinates of the "vertex" (the minimum point in this graph)
by substituting the x = -2 into the equation.
y = (-2)2 + 4(-2) - 5
y = 4 - 8 - 5
y = -9
Vertex: (-2,-9)

Parabola:   y = -x2 + x + 6
Axis of symmetry: symmetryeq
aanew
quassypic2a

Determine the coordinates of the "vertex" (the maximum point in this graph)
by substituting the x = ½ into the equation.
y = -(½)2 + ½ + 6
y = -¼ + ½ + 6
y = 6¼
Vertex: (½, 6¼)

ti84c
For calculator help with graphing parabolas
click here.


divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".