|
Directions: Questions for Parts II, III, and IV are long response questions. You will need paper, pencil and a graphing calculator to work out the problems. Check your answer after solving each problem by clicking the ANSWER button.
 Appropriate for New York Next Generation Standards |
25. Write the equation 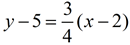 in the equivalent form most appropriate for identifying the slope and the y-intercept of the function. |
|
|
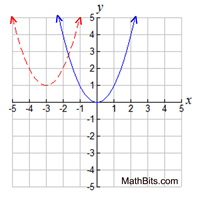
26. The graph of y = x2 is shown (the solid drawing) at the right. Write the equation for the graph of the transformation of this function (the dotted drawing) which shifts the function three units to the left and one unit up. |
 |
|
|
27. Explain why a function has only one y-intercept. |
|
|
28. Solve using the quadratic formula: 9x2 + 3x - 2 = 0 |
|
|
29. Rationalize and simplify:  |
|
|
30. Express the area of a rectangle with length (4x3 + 2x2 + x + 1) and width (x2 - 3). (Express answer in expanded form.) |
|
|
31. A drawing shows a series of the same size blocks. The first row has 2 blocks, the second row has 4 blocks and the third row has 8 blocks. If the drawing continues increasing in this same pattern, how many blocks will be in the 15th row? |
|
|
32. State whether  is rational or irrational. Explain. |
|
|
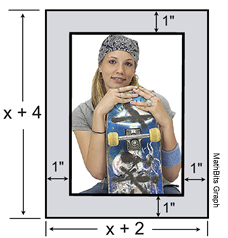
33. Taylor places a one inch frame around the picture taken of her competition win.
The height of the picture, with the frame, is represented by x + 4, and the width is represented by x + 2.
a) Express, in terms of x, the height and width of the picture, without the frame, in inches. Label each answer.
b) Express, in terms of x, the area of the picture, without the frame, in square inches.
c) Express, in terms of x, the area of the picture and the frame together, in square inches |
 |
|
|
34. Dino is 5 years older than his canine sister Bella. The product of their ages is 36.
a) Write an equation to model this situation.
|
b) Find Bella's age using algebra. |
|
|
35. Graph the inequality system: y < x + 3 and 2x + y < 0.
a) Label the solution set S. |
b) Is the point (4,-3) in the solution set? |
|
|
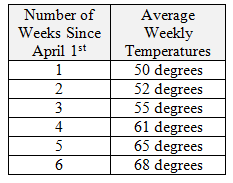
36. Average weekly temperatures in central New York were recorded beginning April 1st, as shown. |
a) Find a linear regression equation for this data. Round all coefficients to nearest hundredths.
b) Based upon your regression equation, predict the average weekly temperature 10 weeks after April 1st (to nearest degree).
c) State the correlation coefficient, to nearest hundredths, and indicate its strength.
|
 |
|
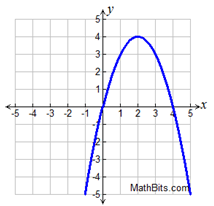
37. While jogging, Kevin turns his head to see a friend waving from a passing car. Unfortunately, he did not notice that he was jogging directly into a five foot tall roadside delimiter marker. After hitting the post,
Kevin falls to the ground where his front tooth is dislodged and flies upward into the air. The height attained
by the tooth during its airborne journey is shown in the graph at the right. The x-axis represents the time in seconds and the y-axis the height in feet.
|
|
a) The tooth’s journey is a transformation of the function y = x2. Write an equation to represent the tooth’s journey.
b) Based upon the information given, place constraints upon your new equation so the graph depicts only the actual heights attained by the tooth.
c) What was the maximum height reached by the tooth? |
d) During what interval was the height of the tooth decreasing?
e) How long did it take for the tooth to return to the ground? |
|
|
|
|
