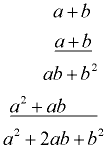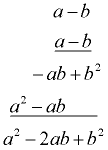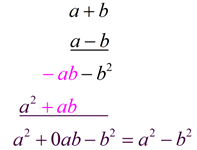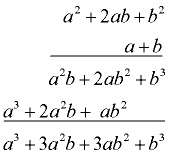|
There are certain binomial multiplications that appear over and over again in problems and on tests. If you can remember the patterns, you will be able to quickly arrive at these products and save yourself some work. But don't worry! If you cannot remember these patterns, you can always multiply the binomials to arrive at the answer.
 Squaring a Binomial: (multiply a binomial times itself)
(a + b)² = a² + 2ab + b²
(a − b)² = a² − 2ab + b²
In each pattern, the middle term is twice the multiplication of the terms used to create the binomial expression. Notice how the sign of the middle term is positive in (a + b)², and negative in (a - b)². |
Vertical Method Check:
If you forget these patterns, just multiply the binomials:
  |
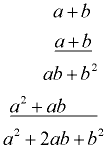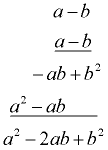Horizontal Method Check:
: (a + b)2 = (a + b)(a + b)
= a•a + a•b + b•a + b•b
= a2 + 2ab + b2 |
(a - b)2 = (a - b)(a - b)
= a•a - a•b - b•a + b•b
= a2 - 2ab + b2 |
|
|
(a + b)2 ≠ a2 + b2
(a - b)2 ≠ a2 - b2 |
Be careful! While this may look like a good idea,
it is NOT true! |
|
If you still think (a + b)2 will equal a2 + b2, try substituting
a = 2 and b = 1 and see if it works.
(2 + 1)2 ≠ 22 + 12
32 ≠ 4+ 1 ;
9 ≠ 5 Oops! |
|
NOTE: Squaring a binomial creates a perfect square trinomial.
A perfect square is created when a value is multiplied times itself
[such as 5 x 5 = 25, making 25 a perfect square].
Thus, (a + b)(a + b) = a² + 2ab + b², making the trinomial a² + 2ab + b² a perfect square.
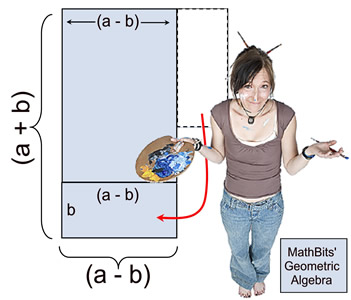
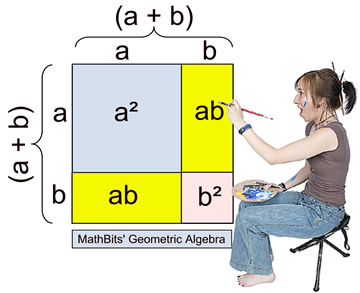
The picture below shows a geometric display
of the square of binomial (a + b). |
|
The picture shows a large square whose sides have a length of (a + b). Inside this square are two smaller squares and two congruent rectangles.
You can see the needed "middle" term when multiplying
(a +b) times (a + b). The picture also shows how the middle term is represented by twice the product of the two terms from the binomial [2(ab) = 2ab].
The area of the large outer square equals the sum of its interior components: (a + b)(a + b) = a² + 2ab + b².
Therefore, (a + b)² = a² + 2ab + b² |
 |
Examples for Squaring Binomials:
|
(x + 4)² |
= (x + 4)(x + 4) |
| |
= x² + 4x + 4x + 16 |
| |
= x² + 8x + 16 |
Notice the middle term = twice [x • 4], or 2(4x) = 8x. |
|
(2x - 3)² |
= (2x - 3)(2x - 3) |
| |
= 4x² - 6x - 6x + 9 |
| |
= 4x² - 12x + 9 |
Notice the middle term = twice [2x•(-3)] = -12x. |
Product of Sum and Difference of the Same Two Terms: (These binomials differ only by the sign of the second term and are called binomial conjugates.)
(a + b)(a - b) = a² - b²
While there appears to be "no" middle term in this pattern to form a trinomial, the truth is that the coefficient of the middle term is zero, and is therefore not written.
(a + b)(a - b) = a² - ab + ab - b² = a² - b²
[-ab + ab = 0ab]
|
If you forget this pattern, just multiply the binomials:
 |
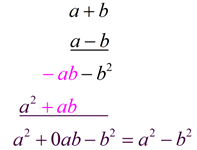NOTE: The product of conjugate binomial pairs, (a + b)(a - b) = a² - b²,
produces the difference of perfect squares.
You will want to remember this pattern which creates a zero coefficient on the middle trinomial term.
It will prove most helpful when factoring and solving other types of problems.
Let's take a geometric look at a2 - b2.
We will assume a > b for this investigation.
 |
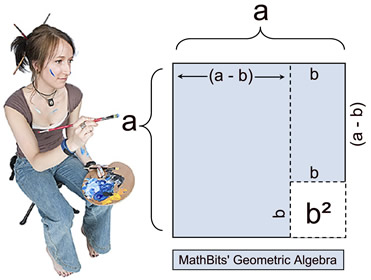In this first diagram, we see a square whose sides are of length "a".
From that large square, a smaller square whose sides are of length "b" is cut from the lower right corner.
The remaining shaded section represents
a2 - b2. But it is unclear how this is related to (a + b) and (a - b). |
Using the diagram above, we are going to "slide" the small shaded rectangle on the top right side (with dimensions (a -b) and b), down "under" the left portion of the diagram.
We can see that the dimension of (a - b) will coincide with the (a - b) length of the bottom of the left side.
Now, it can be observed that the shaded portion representing a2 - b2 can become the shaded portion representing (a + b)(a - b). |
|
|
What about a2 + b2 ?
Doesn't it equal something? |
Actually, it does. But it requires more skills than we will cover in this course. |
Examples for Multiplying Binomial Conjugates:
|
(x + 2)(x - 2) |
= x² - 4x + 4x - 4 |
| |
= x² - 4 |
Notice the middle term has a coefficient of 0. |
|
(2a + 5)(2a - 5) |
= 4a² - 10a + 10a - 25 |
| |
= 4a² - 25 |
Notice the middle term has a coefficient of 0. |
The last set of patterns relates to cubing binomials.
Remember that "cubing" is the process of raising a value to the power of 3.
It means to multiply a value times itself three times, such as 123 = 12 • 12 • 12.
Cubing a Binomial:
(multiplying the binomial times itself 3 times)
Algebra 1:
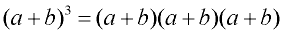
To cube a binomial, multiply it times itself three times. This will require a two step process.
STEP 1: Multiply the first two factors.
STEP 2: Multiply your answer by the third factor. |
STEP 1:
Multiply the first two factors.
|
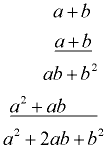
STEP 2:
Multiply STEP 1 by the third factor.
|
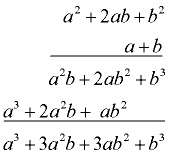
Algebra 2:
CASE 1:
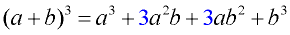
Notice the pattern:
1. There are 4 terms in the pattern.
2. The exponents of a decrease in each term, while the exponents of b increase in each term.
3. The middle terms contain a factor of 3.
|
Algebra 2:
CASE: 2
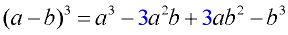
The pattern is similar to CASE 1, but the signs of the second and fourth terms are negative.
Remember: if you forget the patterns, just multiply the three factors to get the answer. |
Example for Cubing a Binomial:
|
(x + 1)3 |
= (x + 1)(x + 1)(x + 1) |
| |
= (x² + 2x + 1)(x + 1) |
| |
= x3 + 3x2 + 3x + 1 |
Algebra 1 method. |
| |
|
| |
(x + 1)3 |
= x3 + 3(x²)(1) + 3(x)(1²) + 13 |
| |
= x3 + 3x2 + 3x + 1 |
Algebra 2 method with pattern. |
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
