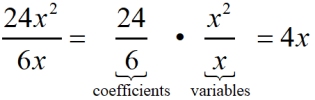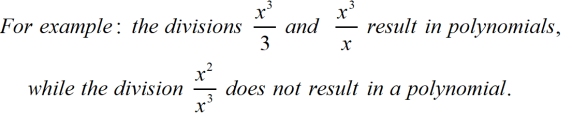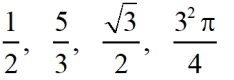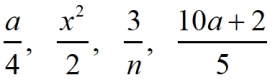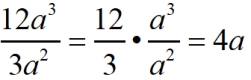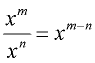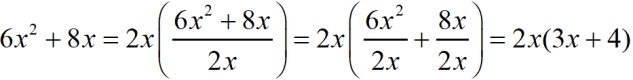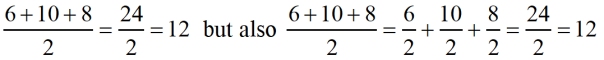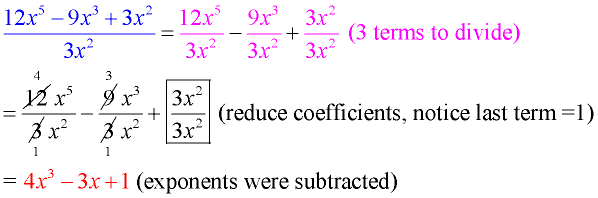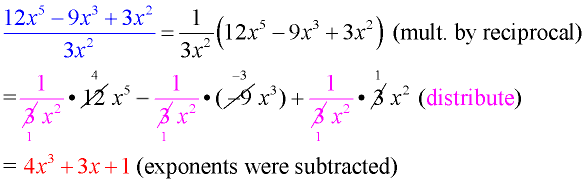|
NOTE: In Algebra 1, "division of polynomials" is not addressed as an in-depth topic. Polynomial division has, however, already been seen when dealing with topics such as ratios, algebraic expressions, rules of exponents, and factoring. (Keep in mind that the fraction bar symbolizes division.) On this page we will take a look at some familiar problems, as seen through the lens of division. (None of the examples allow division by zero.)
|
 A monomial is a polynomial with only one term. A monomial is a polynomial with only one term.
(No add or subtract signs between terms. No negative exponents. No variables in the denominator.) |
Since a monomial is a polynomial, it possesses all of the properties of a polynomial.
A monomial must have whole number exponents, and no variables in its denominator.
Remember that the set of polynomials is not closed under division.
That is, when a
polynomial is divided by another polynomial,
the result may, or may not, be
another polynomial
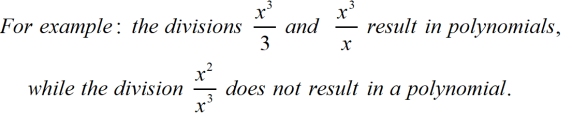
The last term, above, is not a polynomial because it retains a variable in its denominator after being reduced.
So, where have we already seen "division by a monomial",
but may not have thought of it as "division"? |
 |
Ratios and Rational Expressions:
Remember that the fraction bar represents "division", so all of these examples are actually polynomial division.
|
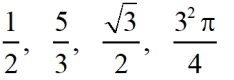
The monomial divisors are 2, 3, 2, and 4.
|
Algebraic Expressions:
Now, we start to see variables used in fractional forms, such as
"monomial a divided by monomial 4".
The variable may even be the divisor, such as "monomial 3 divided by monomial n". |
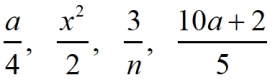
"n" is not equal to zero in this example.
The monomial divisors are 4, 2, n, and 5. |
Working with Exponents:
(with Algebraic Expressions)
Dividing a polynomial (monomial) by a monomial was seen in the section on "Exponents". |
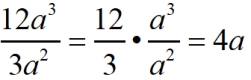
"a" is not equal to zero in this example.
The monomial divisor is 3a2. |
Remember to divide the numbers out front (the coefficients),
and then divide the variables by using the quotient rule for exponents. |
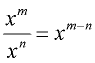 |
Factoring:
When you are "pulling out" (factoring out) the Greatest Common Factor, you are actually dividing the expression by that GCF to find the other remaining factor.
In this example, the GCF = 2x, so the entire expression is divided by 2x to find (3x + 4). |
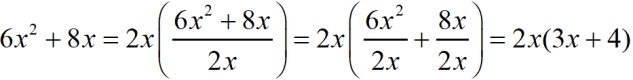
"x" is not equal to zero in this problem. The monomial divisor is 2x.
|

For algebraic expressions,
when dividing a monomial by a monomial,
remember to divide the numbers out front (the coefficients),
and then divide the variables by using the quotient rule for exponents
(i.e., subtract the exponents, top exponent minus bottom exponent).
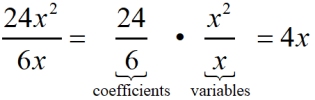

Be aware when dividing a polynomial by a monomial.
Consider the following:
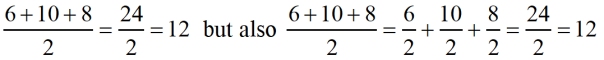
The divisor of 2 in this example is actually the common denominator
for all 3 terms in the numerator.
This concept, of assigning the common denominator to EACH term in the numerator,
will be particularly useful when working with algebraic expressions.
 When dividing a polynomial by a monomial, When dividing a polynomial by a monomial,
divide EACH term of the polynomial by the monomial.
Remember to use the quotient rule for exponents. 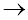
|
|

When dividing a polynomial by a monomial, the number of terms in the polynomial equals the number of terms in the answer. |
|
|
Remember, when dividing a term by itself, the result is one. It does not cancel out and disappear. |
|

|
Let's write this division problem as a fraction:
• The numerator of a fraction will be the first polynomial from the example, and the denominator of the fraction will be the second monomial from the example.
• Now, create three separate fractions with the same denominator.
• Since there are 3 terms in the polynomial numerator, there will be three terms in the answer.
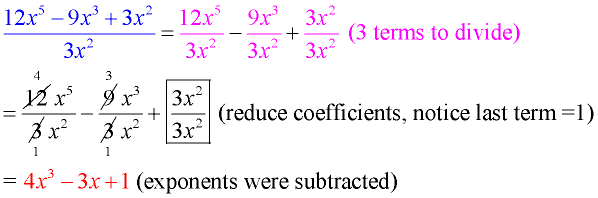 |

FYI: Another way of looking at "dividing by a monomial" is multiplying by the reciprocal of the monomial. See Example 2 below where the reciprocal of 3x2 is being multiplied as 1/(3x2).
|
|
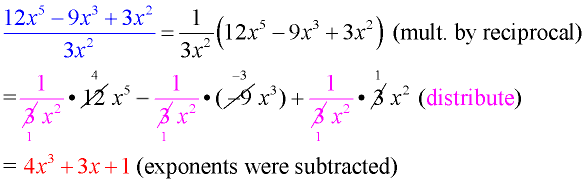 |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|