|
| NOTE: You have done a lot of work with solving equations in your previous math classes. This page is going to be a quick overview of the types of equations that should look familiar to you. If you need a "review" of your previous skills, check out the "Refreshers"section at the bottom of the Topic Outline page. |
|
An equation states that numerical expressions or algebraic expressions are equal.
Linear equations are equations of degree one, where the variable's exponent is one.
|
|
Solving a linear equation is a process of using "inverse" operations to undo the operations that have been applied to the variable when the equation was created.
(addition and subtraction are inverse operations)
(multiplication and division are inverse operations)
One can "undo" the other!
Your goal is to isolate the variable (get it alone) on one side of the equal sign and solve the equation.
You must always make the same changes to BOTH sides of the equal sign to "balance the equation".
Let's take a look at the types of equations that should look familiar to you. |
 |
|
 Solving equations with variables on both sides of the equal sign:
Solve for x: 6x + 8 = x - 12 |
|
Analysis: This equation has variables on both sides of the equal sign. We need to get the x's combined into one term on one side.
"It will be easier to move" the variable with the smaller coefficient (the number multiplied times it), which in this case is the x term on the right. The sign in front of this x-term is implied to be a positive one, and one is smaller than 6, so move this term.
Subtract x from both sides.
Now, proceed as shown in the two-step example above.
|
|
 |
When like-variables are scattered throughout a problem, you must get the variables together on one side of the equal sign before you can solve. |
|
Check answer: |
Check:
6x + 8 = x - 12
6(-4) + 8 = (-4) - 12
-24 + 8 = -4 - 12
-16 = -16 True!
|
|
Rather than showing all of the steps in solving an equation, some students simply think of "moving" terms across the equal sign. If you think of equations in this manner, remember that moving any term across the "equal sign" changes the term's sign. You may want to think of the = sign as a bridge. Any value crossing the bridge changes its sign.
|
|
Solving equations with multiple variables on one side of equal sign:
Solve for x: 8a + 1 - 4a + 7 = 3a + 10 |
|
Analysis: This equation has more than one term containing "a" on the left side of the equal sign. We need to get the a's combined into one term on the left side before continuing.
"Make the problem as simple as possible by combining any like terms on either side before solving."
8a + 1 - 4a + 7 = 3a + 10
8a - 4a + 1 + 7 = 3a + 10
4a + 8 = 3a + 10
Now, proceed as in the last example.
|
|
|
When combining terms, be sure to "take along" the sign in front of the term. If there is no visible sign in front of a term, it is considered to be +. |
|
Check answer:
Always check back into the original equation:
8a + 1 - 4a + 7 = 3a + 10
Do not use the combined equation:
4a + 8 = 3a + 10
You may have made an error in the creation of the "combined equation" that will not show up unless you check in the original equation.
|
Check:
8a + 1 - 4a + 7 = 3a + 10
8(2) + 1 - 4(2) + 7 = 3(2) + 10
16 + 1 - 8 + 7 = 6 + 10
16 = 16 True!
|
Solving equations containing parentheses:
Solve for m: 2(m + 10) = 4(m - 15) |
|
Analysis: This equation contains parentheses.
The first step is to get rid of the parentheses. In this problem, you need to multiply through (or across) the parentheses.
Distribute across the parentheses to get rid of the parentheses.
Now, proceed as shown in the examples above.
|
|
|
When parentheses are involved in the solution of an equation, remember the distributive property. |
|
Check answer: |
Check:
2(m + 10) = 4(m - 15)
2(40 + 10) =4(40 - 15)
2(50) = 4(25)
100 = 100 True!
|
|
If you see an equation like 5x - (3x + 2) = 14, remember that there is an implied "1" in front of the parentheses.
5x - 1(3x + 2) = 14
Distribute "-1", being careful of the signs.
5x - 3x - 2 = 14 (the solution is x = 8.)
|
|
Solving equations containing decimals:
Solve for x: 4x + 2.6 = 3x + 8.1 |
|
Analysis: Equations may contain decimals as constants (as seen here) or as coefficients.
There is no secret to solving problems with decimals. Simply solve as you would solve an equation with integer values.
Proceed as shown in the examples above.
|
|
Check answer: |
Check:
4x + 2.6 = 3x + 8.1
4(5.5) + 2.6 =3(5.5) + 8.1
22 + 2.6 =16.5 + 8.1
24.6 = 24.6 True!
|
|
When solving equations with decimals, you can multiply all terms by a power of 10 that will remove the decimal points from the problem. Be sure you remove any parentheses from a problem before attempting this type of approach. Be sure to multiply carefully. The example above needs the use of 10 to the power of one.
10 • 4x +10 • 2.6 = 10 • 3x + 10 • 8.1
40x + 26 = 30x + 81 ; 10x = 55 ; x = 5.5
|
|
Solving equations containing fractions:
Solve for x:  |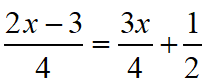
Method:
removing fractions. |
| Analysis: Our goal is to remove the fractions from this problem.
In this solution Method, we will find the least common denominator (LCD) for all fractions, and then multiplying EACH side of the equation by that common denominator.
The common denominator is 4, so multiply both sides of the equation by 4.
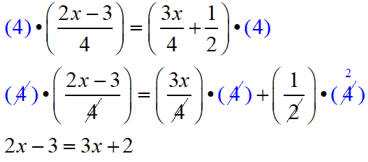
Now, solve this equation. |
Multiply through by 4
to remove the fraction:
|
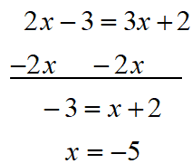
Check answer: [Always "check" back into the original equation, NOT the new equation.] |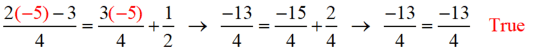
|
In this example, you could have multiplied EACH TERM times 4 when you started. In so doing, be careful to notice that the left side of the equation is ONE term, while the right side of the equation is TWO terms.
In addition, you always have the option of "keeping" the fractions, but the chances of errors is usually greater.
|
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
