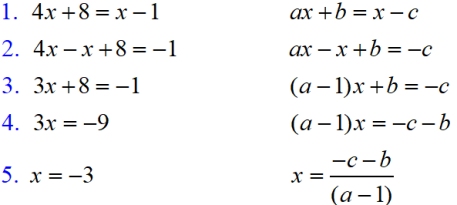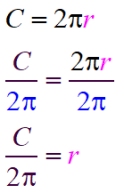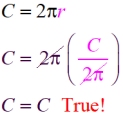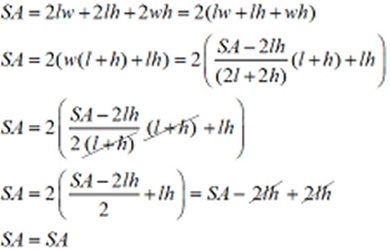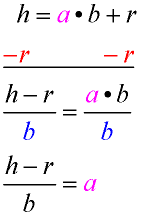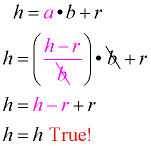|
A literal equation is an equation with several variables (letters).
One of the letters will be the variable we are interested in examining.
The other letters may represent other varying values or they may be constants.
Literal equations may be referred to, in some instances, as simply "formulas".
The Pythagorean Theorem formula c2 = a2 + b2 is an example of a literal equation.

|
|
The key to solving literal equations
is keeping your eye on the variable
you need to represent. |
|
When working with literal equations, your task will be to solve for one of the variables, in terms of the other variables. The question will state which variable you are to find. Concentrate on that variable, and treat all of the other variables as constants. Just pretend the other variables are numbers. You can think of this process as "highlighting" a specific quantity in an equation.
The methods used to solve literal equations are the same as the methods you have already learned to solve equations.

Let's compare an equation that we are familiar with solving, (4x + 8 = x - 1),
with a literal style of that same equation, (ax + b = x - c).
In each case, we are solving for x.
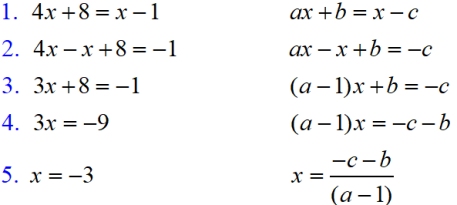 |
1 Given equation.
2. Subtract x from both sides.
3. Get coefficient of x.
4. Subtract 8 (or b) from both sides.
5. Divide by coefficient of x. |
You can see that the steps in each solution are the same.
Just remember to focus on the variable being highlighted (solved for),
and proceed as you normally would for
solving any equation of this format.


This example will isolate ("highlight") a specific variable in a formula.
Formula for the circumference of a circle:
Solve the r in terms of C: C = 2πr |
|
Analysis: Focus on the "r ".
We need to isolate the "r" on one side of the equal sign.
(It does not matter if you isolate r on the right side or on the left side.)
Remove the multiplied "2π", from in front of r, by dividing both sides by "2π".
Express the answer, which is in terms of "C ".
|
|
 |
When solving literal equations, FOCUS on the needed variable and solve as usual. |
|
Check answer: Yes, you can check these answers.
Start with the original equation.
Substitute into the original equation, the "new" equivalent value you found for r. In this case, r = C/(2π).
When simplified, a "true" statement should be found.
|
Check:
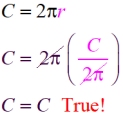
|


This example will also solve for a specific variable in a formula, but the work involved is a bit more complex.
Formula for surface area of a rectangular prism:
Solve for w. SA = 2lw + 2lh + 2wh |
|
Analysis: Focus on the "w".
We need to isolate the "w".
Remove the added "2lh" by subtracting "2lh" from both sides.
Factor out the "w" on the right side.
Remove the multiplied "(2l + 2h)" by dividing by that value.
Express the answer, which is in terms of "SA", "l" and "h".
|
|
 |
Again, when solving literal equations, FOCUS on the needed variable and solve as usual. You may need to employ more of your math skills. |
|
Check answer: Due to the fractional answer, this check is a bit more involved. We will factor the equation first, and then substitute in an effort to make the substitution easier.
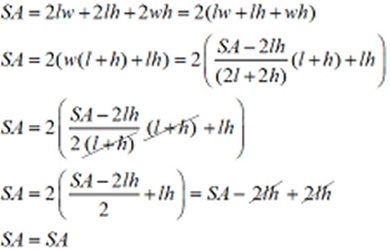 |


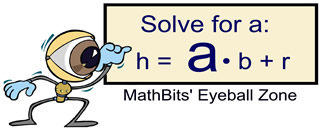
Solving a literal equation does not have to be associated with a known formula. Consider the example below.
Solve for a: h = a • b + r |
|
Analysis: Focus on the "a".
We need to isolate the "a".
Remove the added "r" by subtracting "r" from both sides.
Remove the multiplied "b" by dividing both sides by "b".
Express the answer, which is in terms of "h", "r" and "b".
|
|
 |
As we have done before, we FOCUS on the needed variable and solve as we normally would solve. |
|
Check answer: |
Check:
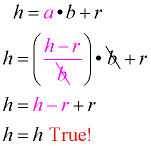
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|