|
| What happens as the slope of a function changes? (with the y-intercept not changing) |
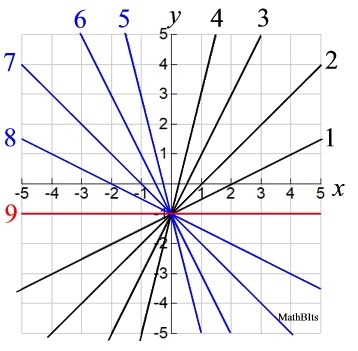
Graphed at the right:
1. f (x) = 0.5x - 1
2. f (x) = x - 1
3. f (x) = 2x - 1
4. f (x) = 4x - 1 |
(Increasing)
|
5. f (x) = -4x - 1
6. f (x) = -2x - 1
7. f (x) = -x - 1
8. f (x) = -0.5x - 1
|
(Decreasing) |
| 9. f (x) = 0x - 1 |
(Horizontal) |
|
f (x) = mx + b is increasing, if m > 0.
f (x) = mx + b is decreasing, if m < 0.
f (x) = mx + b is constant, if m = 0. |
|
In this problem, all graphs cross the y-axis at the point (0,-1) because the "b" value is always -1.
POSITIVE SLOPE: When the slope, m, is greater than zero, a line goes up (from lower left to upper right) across the graph. The y-values increase. The larger the slope, the faster the rate of change, and the faster the line goes up.
Lines with extremely small positve slopes start to look "flat" (horizontal), but never actually become flat.
Lines with extremely large positive slopes start to look straight up-and-down (vertical), but are never vertical.
NEGATIVE SLOPE: When the slope, m, is less than zero, a line goes down (from upper left to lower right) across the graph. The y-values decrease.
The more negative the slope, the faster the line goes down (drops).
As slope becomes extremely less negative (such as m = -0.005), lines start to look "flat" (horizontal), but never actually become flat.
As slope becomes extremely more negative (such as m = -500), lines start to look straight up-and-down (vertical), but never become vertical.
ZERO SLOPE: When the slope, m, is zero, the line is horizontal. The y-values remain the same across the entire graph. The graph is constant (never changing in its y-value).

| What happens as the y-intercept of a function changes? (with the slope not changing) |
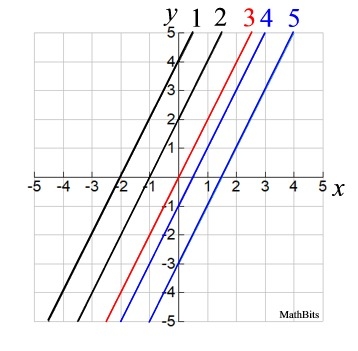
Graphed at the right:
1. f (x) = 2x + 4
2. f (x) = 2x + 2
3. f (x) = 2x
4. f (x) = 2x - 1
5. f (x) = 2x - 3 |
|
Since the slope (steepness) never changes, these lines are parallel.
Parallel lines have the same slope. |
|
The rate of change (slope m) is the same for all of these lines.
The only difference is where the lines cross the y-axis.
|

Which graph corresponds to which equation?
Use your knowledge of slopes and y-intercepts to make these matches. |
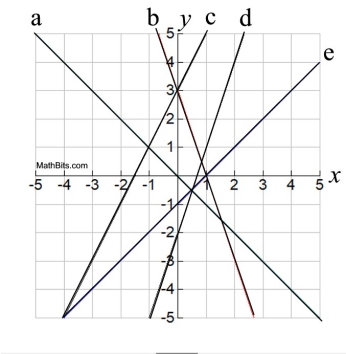
Graphed at the right:
1. f (x) = 2x + 3
2. g (x) = 3x - 2
3. h (x) = -3x + 3
4. k (x) = x - 1
5. m (x) = -x |
|
It is amazing how quickly you can identify the matches, since these equations are in
y = mx + b form. |
|
Think y = mx + b.
Check the y-intercepts (b) and whether the slope (m) is positive (increasing) or negative (decreasing)
and you can identify the lines quickly.
| Answers: 1-c, 2-d, 3-b, 4-e, 5-a |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|



