If you are asked to determine if a specific "value" (number) is a solution to an inequality,
there are two likely situations that may occur.
1. You are given the statement of an algebraic
inequality.
2. You are given a graphic display of an inequality.
| 1. Given the Statement of an Algebraic Inequality: |
When asked if a value "is a solution" to an inequality, you are being asked if the value "makes the inequality true".
In this section, we will be doing "direct substitution" into an inequality of algebraic expressions
to determine if the numerical value is a solution for the inequality.
(While it is an option, we will not be "solving the inequalities for the variable" on this page.)

Given: 2x + 3 < 3(2x - 3)
Are the following values "solutions" for this inequality? |
The question is asking ...
Do these values make the inequality TRUE?
a) x = 5
2x + 3 < 3(2x - 3)
2(5) + 3 < 3(2(5) - 3)
10 + 3 < 30 - 9
13 < 21 TRUE: x = 5 is a solution.
b) x = -2
2x + 3 < 3(2x - 3)
2(-2) + 3 < 3(2(-2) - 3)
-4 + 3 < -12 - 9
-1 < -21 FALSE: x = -2 is NOT a solution.
c) x = 3
2x + 3 < 3(2x - 3)
2(3) + 3 < 3(2(3) - 3)
6 + 3 < 18 - 9
9 < 9 FALSE: x = 3 is NOT a solution.
d) x = 10
2x + 3 < 3(2x - 3)
2(10) + 3 < 3(2(10) - 3)
20 + 3 < 60 - 9
23 < 51 TRUE: x = 10 is a solution.
|
Substitute the given x-values directly into the inequality to see if the resulting statement is true.
Evaluate the algebraic inequality as you would a linear algebraic expression.
Things to notice:
• Be careful when dealing with negative results. Remember how negative numbers are placed on the number line, where values to the right are always larger.
• Inequalities may have more than ONE solution. There actually may be infinite numbers of answers. Think about what number line graphs of inequalities look like.
•
This inequality would be fairly easy to solve so that x is isolated on one side of the inequality symbol. Since we have 4 values to check, this would be an option. |


Given: 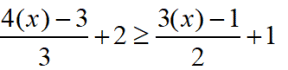
Are the following values "solutions" for this inequality? |
The question is asking ...
Do these values make the inequality TRUE?
a) x = 3
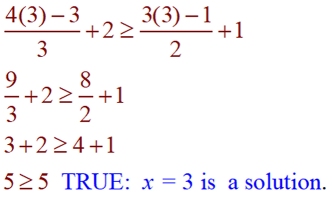
b) x = 1
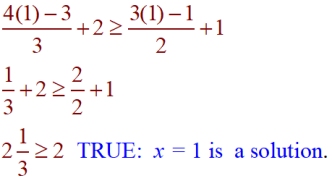
|
Things to notice:
• Unlike the last problem, this inequality will not lend itself to a fast and easy solution for isolating x on one side of the inequality symbol. It can be done, but will take some time.
Direct substitution for the two values will be faster.
• Again, we see that there can be numerous solutions to this one inequality.
• Don't be scared off by fractions. Fractions are perfectly viable candidates when working with inequalities.
|


Elena must score an average of at least 90 in Math to compete in the Math Olympiad. Her current math test scores are 81, 85, 91, and 97, and 90 on the first five tests. She will be taking one more test. Her situation can be modeled by the inequality: 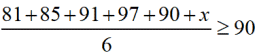
Will a score of 92 on the upcoming test be sufficient for Elena to participate in the Math Olympiad?
|
The question is asking ...
Does 92 make the inequality TRUE?
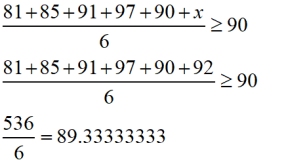
Since 89.33333333 is not greater than or equal
to 90, the score of 92 is not sufficient.
|
Things to notice:
• In a word problem, such as this, it would be unnecessary to "solve" the inequality to isolate x on one side of the inequality symbol. Since only ONE situation is going to be examined, it will be faster to simply substitute the number 92 into the existing inequality to determine the result.
If the question "asked" you to also solve for x, then you would need to solve for x as well as determine the value of 92.
|

| 2. Given the Graph of an Inequality: |
When asked if a value "is a solution" to an inequality graph, you are being asked if the value "lies in the SHADED portions of the graph".
The shaded portions of a graph will include any closed circles and any solid lines.
It will not include open circles, dashed lines, or unshaded sections.

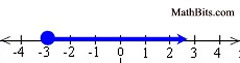
Are the following "values" solutions for the inequality graph shown below?
 |
The question is asking ...
Do these values fall within the shaded regions of this inequality graph?
a) x = 5
Yes, the arrow indicates that the shaded bar will continued to the right side of the graph.
YES: x = 5 is a solution.
b) x = -3
Yes, the circle at -3 is shaded (closed), making it part of the solution to the inequality.1 < -21 YES: x = -3 is a solution.
c) x = -6
No, -6 will not be covered (shaded) by the bar so it is not part of the solution.
NO: x = -6 is NOT a solution.
|
Examine the number line to see if the shaded bar included the values being examined. Remember that a closed circle means that value is included in the solution.
Things to notice:
• Reading solutions from a number line is fast and easy.
• If the value being examined is off the visible graph, remember to check the arrow on the bar to see in which direction it continues.
|


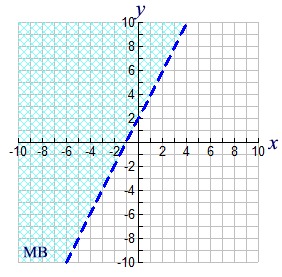
Are the following "(x,y) values" solutions for the inequality graph shown at the right?
|
 |
The question is asking ...
Do these coordinates fall within the shaded region of this inequality graph?
a) (1,8)
Yes, the point falls in the blue shaded region.
YES: (1,8) is a solution.
b) (0,2)
No, the point falls on the "dashed" straight line, meaning it is not part of the solution.
NO: (0,2) is NOT a solution.
c) (-5,-5)
Yes, the point falls in the blue shaded region.
YES: (-5,-5) is a solution.
d) (-22,15)
Yes, the point will be in the shaded half plane of the graph.
YES: (-22,15) is a solution.
e) (-1, -6)
No, the point does not fall in the shaded region.
NO: (-1,-6) is NOT a solution.
|
Things to notice:
• The straight line boundary in this graph is dashed, meaning it is not included in the solution.
• If the value being examined is off the visual view of the graph, remember that the straight line boundary is dividing the entire plane in half. Make your decisions accordingly.
• Again, graphs are easy to read and the solutions can be verified quickly.
|

|