|
We saw under Functional Notation that y = 3x + 2 and f (x) = 3x + 2 can be interpreted as equivalent notations, where y has been replaced by f (x), or y = f (x).
In
y = 3x + 2, we see "y as a function of x".
In f (x) = 3x + 2, we see the notation indicating the existence of a function with x as input.
Since functions represent the "relationships between variables",
we can expand this notation concept to rewriting certain types of equations.
Things to keep in mind:
• Not ALL equations are functions (consider x + 2 = 8 : only 1 variable that is graphically a vertical line)
• Not ALL functions are represented as equations (some are graphical displays).
• Remember, that in f (x) = 3x + 2, the variable x, shown in f (x), is the same as the variable used in the expression 3x + 2. This is the independent variable. Keep this in mind!
|
|
|
Let's take a look at some equations, in two variables,
which can be expressed as functions using functional notation.
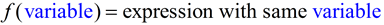
This variable is the independent variable.
These examples will use f as the function name, but any letter(s) may be used.
1. |
Given the equation 2x + y = 15. Write the equation using functional notation with x as the independent variable.
Solution: If the independent variable is to be x, then the functional notation will be f (x) and we will need the "expression" to contain x. We need to solve this equation for y, so that an expression with x remains.
2x + y = 15
y = -2x + 15
Our "expression" will be "-2x + 15" .
Replacing y with f (x), we get f (x) = -2x + 15.
|
2. |
Given a function represented by the equation ½ a + ¾ b = 4. Write the equation using functional notation with b as the independent variable.
Solution: If the independent variable is to be b, then the functional notation will be f (b) and we will need the "expression" to contain b. We need to solve this equation for a, so that an expression with b remains.
½ a + ¾ b= 4
½ a = 4 - ¾ b
a = 8 - 1½ b
In functional notation we have f (b) = 8 - 1½ b.
|
3. |
Given an input value of p, the function f outputs a value q to satisfy the equation 2q + 4p = 82. Write a formula for f (p) in terms of p.
Solution: The variable in the "expression" is to be p. Solve the equation for q, so that an expression with p remains.
2q + 4p = 82
2q = -4p + 82
q = -2p + 41
In functional notation we have f (p) = -2p + 41.
|
|
In plain English ...
... determine the variable needed in the answer (usually given)
... solve for the OTHER variable
... replace your OTHER variable with f (needed variable)
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|


