|
Under Function Basics, we saw the difference between a relation and a function.
In either case, we are dealing with relationships expressed as ordered pairs.
 |
All of the values that can go into a relation or function (input) are called the domain.
All of the values that come out of a relation or function (output) are called the range.
Range may also be referred to as "image".
Note that both relations and functions have domains and ranges. |
The domain is the set of all first elements of ordered pairs (x-coordinates).
The range is the set of all second elements of ordered pairs (y-coordinates).
Only the elements "used" by the relation or function constitute the range.
 |
Domain: all x-values that are to be used (independent values).
Range: all y-values that are used (dependent values). |
|


State the domain and range of the following relation:
{(1,3), (-2,7), (3,-3), (4,5), (1,-3)}.
State whether the relation is a function.
Solution: Domain: {-2, 1, 3, 4}. Range: {-3, 3, 5, 7}.
While these listings appear in ascending order, ordering is not required.
Do not, however, duplicate an element.
No, this relation is not a function. The x-value of "1" had two corresponding y-values (3 and -3).


 |
State the domain and range of the following relation:
(eye color, student's name)
A = {(blue, Steve), (green, Elaine), (brown, Kyle), (blue, Marsha),
(brown, Miranda), (green, Dylan)}
State whether the relation is a function. |
Solution: Domain: {blue, green, brown}. Range: {Steve, Elaine, Marsha, Miranda, Dylan}.
No, this relation is not a function. The eye colors are repeated with different students.


State the domain and range for the elements matched in the diagram below.
State whether the matches form a function.
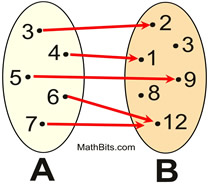 |
Solution: Domain: {3, 4, 5, 6, 7}. Range: {1, 2, 9, 12}.
Note that the range is only the elements that were used.
Yes, the relation {(3,2), (4,1), (5,9), (6,12), (7,12)}is a function.
No x-value has more than one y-value.
FYI: Set B = {1, 2, 3, 8, 9, 12} may be called the co-domain. It is the "possible" set from which output from the relation will fall. The co-domain is NOT necessarily the same as the range. There may be values in the co-domain that are never used. |


State the domain and range associated with the scatter plot shown below.
State whether the scatter plot is a function.
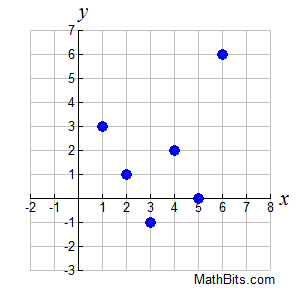 |
Solution: Domain: {1, 2, 3, 4, 5, 6}.
(Be careful not to simply list the domain as 1 < x < 6, which would imply ALL values (including fractions) between 1 and 6 inclusive, unless you specify "x is an integer".)
Range: { 0, -1, 1, 2, 3, 6}
Yes, this is a function. No x-values have more than one associated y-value, and it passes the Vertical Line Test for functions.
Note: Graphs that are composed of a series of dots, instead of a connected curve, are referred to as discrete graphs. A discrete domain is a set of input values that consist of only certain numbers in an interval. |
|

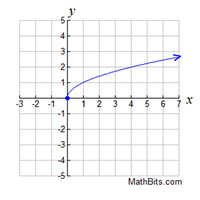
State the domain and range associated with the graph below.
State
whether this relation is a function.
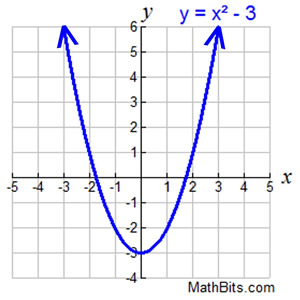 |
Solution: Domain: 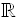 (all real numbers). (all real numbers).
The arrows indicate that the graph continues off the visible grid, so assume that all real numbers are involved.
Range: y > -3 (may also be written as 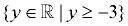 ) )
Yes, this relation is a function, since it passes the Vertical Line Test for functions.
Note: Graphs that are composed of a connected curve are referred to as continuous graphs. A continuous domain is a set of input values that consists of all numbers in an interval. |
|


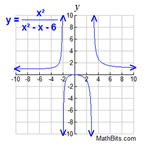
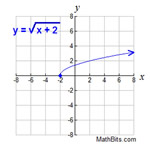
State the appropriate domains for the functions shown below.
When functions are expressed as "rules" (formulas), be sure to think about possible "problem" spots before stating the domain. Remember that the domain is the x-values that are allowed by the function's equation. In most cases, a graph will help show the domain.

 |
It may be necessary to restrict a domain to ensure the existence of a function. |
|
We know not all graphs are functions. As we saw in Example 6, it is often possible, however, to create "functions" from non-function graphs by restricting which domain elements are used.
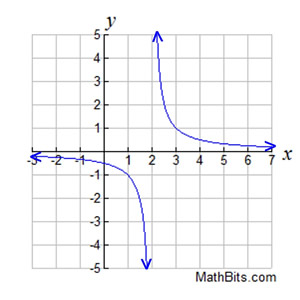 |
The graph at the left is 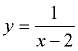 .
At first glance, it appears that this graph passes the Vertical Line Test and is a "function". But it is NOT a function over the domain of Real numbers.
This graph is undefined when x = 2, because substituting two into the function will create a zero denominator.
If we restrict the domain to be "all Real numbers excluding 2", our relation can be called a function.
Domain of the function: 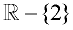 |
 |
It may be necessary to restrict the range to ensure the existence of a function. |
|
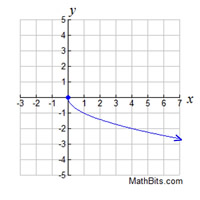
The graph of the relation 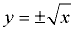 is shown below on the left. It is clear that this relation fails the Vertical Line Test and is NOT a function. We can, however, separate this graph into its two parts and create two separate functions.
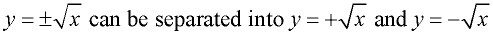
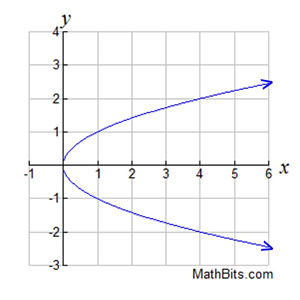 |
|
|
These separated graphs each pass the Vertical Line Test and are functions. The domain for both functions is x > 0. The range of the first function is y > 0, and the second function is y < 0.
|

|
If a domain is not stated, it is generally assumed to be all real numbers.
|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|






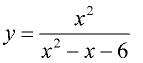

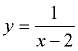 .
.