|
This page is devoted to discussing sequences using function notation.
 |
A sequence is an ordered list. It is a function whose domain is the natural numbers {1, 2, 3, 4, ...}. |
|
Sequence: |
1, |
5, |
9, |
13, |
17, |
21, |
... |
Notation for terms
of the sequence: |
f (1) |
f (2) |
f (3) |
f (4) |
f (5) |
f (6) |
|
 Information about sequences:
• |
Each number in a sequence is called a term, an element or a member. |
• |
Terms are referenced in a subscripted form (indexed), where the natural number subscripts, {1, 2, 3, ...}, refer to the location (position) of the term in the sequence. The first term is denoted f (1), the second term f (2), and so on. The nth term is f (n).
|
• |
The terms in a sequence may, or may not, have a pattern or related formula.
Example: the digits of π form a sequence, but do not have a pattern. |
• |
A functional form of a sequence is represented by f (1), f (2), f (3), ..., f (n),... |
• |
Sequences are functions. |
• |
The domain of a sequence consists of the natural (counting) numbers 1, 2, 3, 4, ... |
• |
The range of a sequence consists of the terms of the sequence. |
• |
When graphed, a sequence is a scatter plot, a series of dots. (Do not connect the dots). |
• |
The sum of the terms of a sequence is called a series.
|
Sequences can be expressed in various forms:
Term Number
|
Term |
Function Notation |
1 |
1 |
f (1) |
2 |
5 |
f (2) |
3 |
9 |
f (3) |
4 |
13 |
f (4) |
5 |
17 |
f (5) |
6 |
21 |
f (6) |
n |
|
f (n) |
|
{1, 5, 9, 13, 17, 21, ...}(list)
Functional notation:
f (n) = 4n - 3 (explicit form)
f (1) = 1; f (n) = f (n - 1) + 4 (recursive form)
Note: Not all functions can be defined by an explicit and/or recursive formula.
|
Forms of sequences:
• |
A finite sequence contains a finite number of terms (a limited number of terms) which can be counted.
Example: {1, 5, 9, 13, 17} (it starts and it stops) |
• |
An infinite sequence contains an infinite number of terms (terms continue without end) which cannot be counted.
Example: {1, 5, 9, 13, 17, 21, ...} (it starts but it does not stop, as indicated by the ellipsis ... ) |
Ways of expressing (defining) sequences:
• |
A sequence may appear as a list (finite or infinite):
Examples: {1, 5, 9, 13, 17} and {1, 5, 9, 13, 17, 21, ...}
Listing makes it easy to see any pattern in the sequence. It will be the only option should the sequence have no pattern. |
• |
A sequence may appear as an explicit formula. An explicit formula designates the nth term of the sequence, f (n), as an expression of n (where n = the term's location).
Example: {1, 5, 9, 13, 17, 21, ...} can be written f (n) = 4n - 3.
|
• |
A sequence may appear as a recursive formula. A recursive formula designates the starting term, f (1), and the nth term of the sequence, f (n) , as an expression containing the previous term (the term before it), f (n - 1).
Example: {1, 5, 9, 13, 17, 21, ...} can be written f (1)= 1; f (n)= f (n - 1) + 4.
|
Graphing Sequences:
Sequence: {1, 5, 9, 13, 17, 21, 25, 29, ...}
• Sequences are functions. They pass the vertical line test for functions.
• The domain consists of the natural numbers, {1,2,3,...}, and the range consists of the terms of the sequence.
• The graph will be in the first quadrant and/or the fourth quadrant (if sequence terms are negative).
|
 |
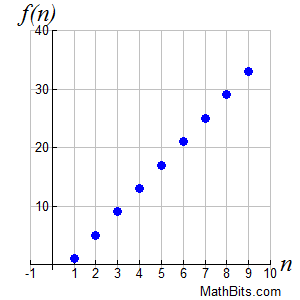• Arithmetic sequences are linear functions. While the n-value increases by a constant value of one, the f (n) value increases by a constant value of d, the common difference. The rate of change is a constant "d over 1", or just d.
• Geometric sequences are exponential functions. While the n-value increases by a constant value of one, the f (n) value increases by multiples of r, the common ratio. The rate of change is not constant, but increases or decreases over the domain. |
|
Arrow down to
"In Func MODE" |
|
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
