|
  Not all trinomials can be factored. Not all trinomials can be factored. |
There are trinomials that simply do not comply with any factoring patterns.
Not all trinomials can be factored over the set of integers,
which means the values of the coefficients of the variables must come from the integers.
Trinomials such as x² + 2x + 7 or 3x² - x - 5 will not play by these factoring rules.
These trinomials, over the set of integers, are called prime polynomials.
They may also be called "irreducible" over the set of integers.
Let's take a look at how we know that these trinomials are not factorable.
| When a = 1: x2 + 2x + 7 |
When a ≠ 1: 3x2 - x - 5 |
Pattern Rule: To find the factors, we need two values that will multiply to the constant term and add to the coefficient of the middle term.
If this trinomial is factorable, we know that there must be two factors of 7 that will add to +2 (since all signs are positive).
Factors of 7:
7 is prime, so we only have 7 • 1
The sum of 7 and 1 is NOT 2.
This trinomial can not be factored.
Examine the graph of y = x2 + 2x + 7.

This graph does not even intersect with the
x-axis.
The expression is not factorable over the set of integers.
|
Factoring by Grouping: To find the factors to split the middle, we need values that multiply to a • c but add to b.
a • c = 3 • 5 = 15
b = -1
Factors of 15:
(one must be positive and one negative)
Sum of possible factors of 15:
+ 15 + -1 = +14
-15 + +1 = -14
5 + -3 = 2
-5 + 3 = -2
No choice adds to -1.
This trinomial can not be factored.
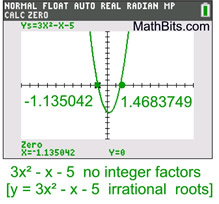
While this graph crosses the x-axis, it crosses at irrational values, whose factors will not be factorable over the set of integers.
The expression is not factorable over the set of integers. |
 When an expression is factorable (over the set of integers), the coefficients of the variable (including constant terms) will be integer values, for both the polynomial and for the factors. When an expression is factorable (over the set of integers), the coefficients of the variable (including constant terms) will be integer values, for both the polynomial and for the factors. |

Also, when polynomial functions are factorable over the set of integers, the coefficients of the variable and the constant terms will be integer values for both the polynomial and for the factors.
The zeros (roots), however, in the polynomial function need not be integers, such as seen in the example below.
These two graphs show functions defined by expressions which are factorable over the set of integers.
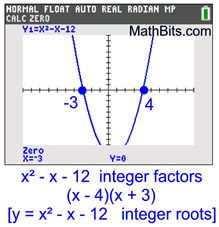 integer roots: {-3, 4}
The coefficients of the variables for both the
integer roots: {-3, 4}
The coefficients of the variables for both the
polynomial and the factors are integers.
In this case the roots also
happen to be integers. |
 rational roots {-2½, 1/3}
The coefficients of the variables for both the
rational roots {-2½, 1/3}
The coefficients of the variables for both the
polynomial and the factors are integers.
In this case, the roots do not
happen to be integers.
|

In the Quadratics section, we will find additional procedures that will be helpful when attempting to factor polynomials that cannot be factored over the set of integers.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|




