Practice Page
Directions: Answer these questions pertaining to factoring polynomials. Choose the best answer.

1.
Squares with side lengths of x feet are cut out of the 4 corners of a rectangular piece of plastic (as shown), which is then folded up to form an open-top box. Express the volume of the box in completely factored form (in cubic feet).


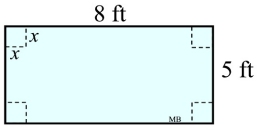
V = l w h
Choose:
x(8 - 2x)(5 - 2x) cu.ft.
4x2(8 - 2x)(5 - 2x) cu.ft.
2x(4 - x)(5 - 2x) cu.ft. 4x(8 - 2x)(5 - 2x) cu.ft.

 

 

2.
A square has an area of 16x2 + 24x + 9 square centimeters. Write an expression for the perimeter of the square in centimeters.
Choose:
(4x + 3)
(12x + 9)
(8x + 6) (16x + 12)

 

 

3.
The sides of a right triangle are labeled as shown.
a) Using the Pythagorean Theorem,
(a2 + b2 = c2), determine which equation can be used to solve for x.
Choose:
x2 + 6x + 7 = 0
x2 + 6x - 7 = 0
x2 + 6x + 9 = 0 x2 + 6x + 25 = 0
 
b) Factor the answer to part a, and set the factors equal to zero to find the roots. What is the length of the side of the triangle represented by x + 3?
Choose:
 
1
 4 7 10


c) Why was it necessary to discard one of the roots?
Choose:
The negative root could not be used as it was an odd number.
The positive root created a value too big to be the triangle's side.
The negative root created a negative length.
The positive root could not be used as it was an odd number.

 

 

4.
A birdbath is to be placed on a concrete slab measuring 10 ft. by 10 ft. The area of the square base of the birdbath is represented by x2 - 6x + 9.

 a) Express the length of one side of the square base in terms of x.
Choose:
(x + 3)
(x - 3)
(x + 3)2 (x - 3)2


b) The concrete slab is to be painted around the birdbath. Express the number of square feet that will need to be painted as the factored difference of two perfect squares.
Choose:
(102 - (x - 3)2)
(102 - (x + 3)2)
(10 - (x - 3))2 (10 - (x + 3))2


c) If x = 6 in this problem, what is the area of the base of the birdbath, and what is the area of concrete to be painted? (Both answers in that order and in square feet.)
Choose:
9 sq.ft.; 100 sq.ft.
9 sq.ft.; 49 sq.ft.
9 sq.ft.; 91 sq.ft. 9 sq.ft.; 169 sq.ft.

 

 

5.
A rectangle has an area represented by
54ab3. If the width is represented by 18ab, which choice represents the length?
      
      Choose:
 
3ab2
3b
3b2
3ab

 

 

6.
In the diagrams shown below, the diagram on the left can "become" the diagram on the right by moving the green rectangle. Which choice interprets what is being modeled?
        
Choose:
a2 +b2   becomes   (a b)(a - b)
a2 - b2   becomes   (a + b)(a - b)  
a2 +b2   becomes   (a + b)(a + b)  
a2 - b2   becomes   (ab)(a - b)  

 

 

7.
The area of a rectangle is expressed as
48x2 + 16x - 15. The area of a square, as shown, is expressed as x2 - 4.
a) Express the square's area in factored form.
Choose:
(x - 2)2
(x + 2)2
(x + 2)(x - 2) (x + 4)(x - 1)
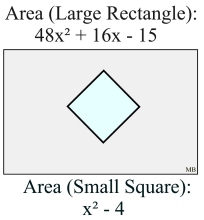b) Express the area of the large rectangle as factored over the set of integers.
Choose:
(4x - 3)(12x + 5)
(12x - 5)(4x + 3)
3(4x - 1)(4x + 5) 3(4x +1)(4x - 5)

c) If the area of the square is subtracted from the area of the large rectangle, the expression for the remaining area would not be factorable.
Choose:
TRUE
FALSE

 

 

8.
If (x + 7) is a factor of 2x2 + 24x + 7m, determine the value of m.
      Choose:
 
m = 5
 m = 10
m = 35
 m = 70

 

 

9.
A rectangular tulip garden has an area represented by 15t2 - 11t - 12.
 a) Express this area as factored over the set of integers.
Choose:
(5t + 3)(3t - 4)
3(5t + 4)(t - 1)
(5t + 6)(3t - 2) (5t - 6)(3t + 2)

b) The narrow 2 foot concrete walkway is built surrounding the garden. Express the area of the walkway.
Choose:
16t + 32
32t + 20
32t + 12 32t + 64


c) The concrete for the walkway has a constant depth of ½ foot.
Express the volume of concrete in cubic feet that was needed to complete the walkway. V = lwh
Choose:
16t + 10
8t + 16.
16t + 32 16t + 6

 

 

10.
Which choice can represent the algebraic difference
(x - 2)2 - (x2 - 4) ?
      Choose:
 
-4(x + 2)
 4(x - 2)
-4(x - 2)
 -4(2 - x)



divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".