Let's take a look at using the "greatest common factor" to factor polynomials.
The greatest common factor will prove to be an important algebraic tool.
 |
The greatest common factor, GCF, is the largest number (or expression) that divides exactly into two or more numbers (or expressions).
It is the largest of the "common factors". |
|
When working with a polynomial expression,
the first step when attempting to "factor completely"
is to determine, and factor out,
the greatest common factor of the polynomial.
 Process: To factor the GCF out of a polynomial
1. Find the greatest common factor of all terms of the polynomial.
2. List each term as the product of the GCF and another factor.
3. Use the distributive property in reverse to factor out the GCF. |
|
 |
| Let's start by factoring out a monomial GCF from a polynomial. |
|
Solution:
|
1. GCF = 3
2. Products using the GCF: 3 • x - 3 • 5
3. ANSWER: 3(x - 5)
|
In Algebra, the process of factoring can often be seen
as the distributive property in reverse.
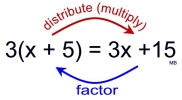
Using the distributive property in reverse,
we can see
(3x + 15) factors into 3(x + 5) with a GCF = 3. |
|
Solution: |
1. GCF = 2x2
2. Products using GCF:2x2 • x2 + 2x2 • 3x - 2x2 • 2
3. ANSWER: 2x2 (2x2+ 3x - 2)
Notice the "distributive property in reverse" at work again.
|
|
You can always tell if your factoring is correct!!
Check your factored answer by multiplying through your answer using the distributive property. The result should be the expression with which you started.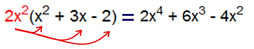 
|
|
Factor: -10a3 + 5a2 - 15a |
|
Solution: |
1. GCF = -5a
2. Products using GCF: (-5a) • 2a2 + (-5a) • (-a) - (-5a) • (-3)
3. ANSWER (-5a)(2a2 - a + 3)
|
|
When the leading coefficient of a polynomial is negative, it is customary to find a greatest common factor which is negative.
(Or think of it as factoring "-1" from each term.)
Watch out for the signs!
|
|
 |
Factor: -20x4 - 50x2 |
|
Solution: |
1. GCF = -10x2
2. Products using the GCF: (-10x2) • 2x2 - (-10x2) • (-5)
3. ANSWER -10x2(2x2 + 5) |
| Let's move on to factoring out a binomial GCF from a polynomial. |
|
Factor: 5x(x + 2) + 9(x + 2) |
|
Solution: |
1. GCF = (x + 2)
2. Products using the GCF: (x + 2) • 5x + (x + 2) • 9
3. ANSWER (x + 2)(5x + 9) |
|
|
Factor: 3a(2a - 1) + 9(2a - 1) |
|
Solution: |
1. GCF = 3(2a - 1)
2. Products using the GCF: 3(2a - 1) • a + 3(2a - 1) • 3
3. ANSWER 3(2a - 1)(a + 3)
|
|
 |
Write (x + 2)(x + 7) + (x + 2)(3x - 2) as a product of two binomials. |
Solution: |
1. GCF = (x + 2)
2. Factoring out (x + 2) gives (x + 2)((x + 7) + (3x - 2))
Combining like terms in the remaining sum gives (4x + 5).
3. ANSWER (x + 2)(4x + 5) |
