1. (3 x 5)3 = 33 x 53 = 3375
Notice that the interior of the parentheses is a product (the multiplication of two terms). Each term is raised to the power of 3.
|
2. (32 x 26)4 = 38 x 224
Apply the "power to a power" rule, as well as this "power of products" rule.
|
3. (abc)4 = a4b4c4
The variables abc are a product a•b•c, so apply the rule to each factor.
|
4. (5a)5 = 55a5 = 3125a5
Notice how the 5 inside the parentheses is also affected by the power of 5.
|
5. (3a2)4 = 34(a2)4 = 34a8 = 81a8
Notice how the "power to a power" rule was used here to raise a2 to the power of 4. |
6. 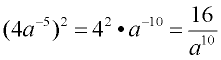
The rule still applies when working with negative exponents.
|
7. 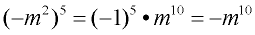
Notice how the negative sign is being handled. The -1 to the power of 5 yields a negative result. |
8. 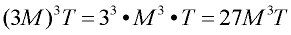
Be sure to apply the exponent to the coefficient of 3.
|
9. 4(2x3)2 = 4•22(x3)2 = 4•4•x6 = 16x6
Notice that the number 4 out in front is not affected by the power of 2 since it is not within the parentheses.
|
10. P = (2K)2W = 22K2W = 4K2W
Formulas often involve working with powers.
|