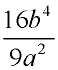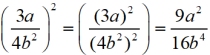As the name suggests, exponentials deal with exponents. |

"Exponential expressions" are identified as a way to write powers in a shorthand form.
They are expressions with exponents. The term "exponential notation" is also used.
In the unit on Exponents, we dealt with these expressions expressed in numerical form and in algebraic form, where the exponent indicates the number of times the base value is multiplied. These expressions were referred to as being in exponential form (or exponential expressions).
In working with exponential expressions, we applied the properties of exponents
to simplify expressions and to verify the equivalence of statements.
Equivalence:
Which choice is equivalent to 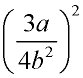 ?
1)
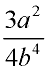 2) 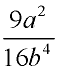 3) 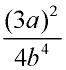 4) 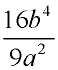
Apply the properties (rules) of working with exponents to solve.
Solution: 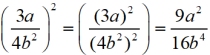 (Choice 2) (Choice 2) |
|
Working with exponentials will involve working with the properties of exponents.
Review RULES associated with Exponents

| Exponential Equations and Functions: |
We know that the exponent associated with a number indicates the number of times
the base number is multiplied.
But what happens when the exponent is a variable?
This is where exponential equations come into play.
When the exponent is a variable (such as x), and it is part of any equation,
you are working with an exponential equation.
 |
An exponential equation is an equation whose exponent (or part of the exponent) is a variable (such as x or 2x + 1). |
|
"Exponential equations" and "exponential functions" deal with a very specific situation.
Only numerical bases with a variable exponent will be considered.

 |
An exponential function is a function having a positive integer (greater than one) as its base and a variable exponent (or part of the exponent). |
|
 |
Equations and functions with a variable as the exponent are
called "exponential equations" and "exponential functions". |
|
While many equations and functions may contain
"exponents"
( such as x2 + 6x + 9 = 0 or y = x2 ),
they are not called "exponential equations" or "exponential functions"
since the exponents are not variables.
They are usually just referred to as "power" equations or functions.
| Here's where the "vocabulary" can get to be a bit confusing: The term "exponential expressions" is generally used to refer to ANY expression containing an exponent, as "the expression is in exponential form" No stipulation is stated for the exponent being a variable. Whereas, the terms "exponential equation:" and "exponential function" refer only to equations or functions that contain variable exponents. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|

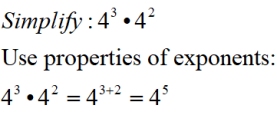
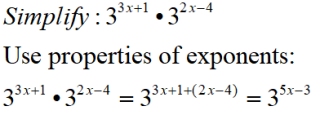
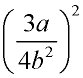 ?
?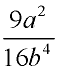 3)
3) 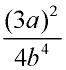 4)
4)