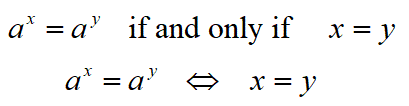|
Note: We will only be examining exponential equations that work with the same base.
More complex equations will be addressed in Algebra 2. |
 |
An exponential equation is an equation whose exponent (or part of the exponent) is a variable (variables such as x or 2x + 1). |
|
Exponential equations can be recognized by the variable in the exponent position.
These equations can have any positive integer as the base number
(but NOT one, since one raised to any power is simply one).
There are different "types" of exponential equations.
We will be dealing with exponential equations that deal with the same base on both sides.
Exponential Property of Equality
When bases are the same, this property applies: 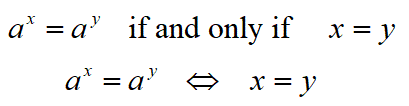 |
When the bases on both sides of an exponential equation are equal,
then the exponents are also equal.

When working with exponential equations, if the bases are same,
set the exponents equal to one another and solve.
1. If 3x = 32, find x.
Since the bases are the same, set the exponents = to one another: x = 2.
This example is just common sense. |
2. If 2x+1 = 24, find x.
Since the bases are the same, set the exponents = to one another: x+1 = 4.
So, x = 3. |
It may be the case that the common bases may be "hidden".
While the equation 2x = 8 may not appear to have common bases,
a closer look will reveal the hidden base on the right side,
8 = 2 • 2 • 2 = 23.
2x = 8 = 23
x = 3 |
 |
3. If 9x+3 = 812x-3, find x.
Rewrite to get the bases the same. 81 = 92.
9x+3 = (92)2x-3
Use the "power raised to a power" rule for exponents (i.e., multiply the powers).
9x+3 = 94x-6
x + 3 = 4x - 6
3x = 9
x = 3
|
4. If 32x+1 = 64, find x.
Get the bases the same. 32 = 25and 64 = 26.
(25)x+1 = 26
Use the "power raised to a power" rule for exponents (i.e., multiply the powers).
25x+5 = 26
5x + 5 = 6
5
x = 1
x = 1/5 |
Did you notice how finding these solutions involved creating equivalent
exponential expressions when searching for the common base value?
812x-3 is equivalent to 94x-6

Steps to solving an exponential equation
with common bases.
1. Express both sides in terms of the same base.
2. Set the exponents equal
3. Solve for the variable. |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|