30% of 590 = 0.30 • 590
= $177 lost in value after one year.
Subtract this monetary loss from the price of the new scooter to find the value of the scooter at the end of one year.
590 - 177 = $413 is the value of the scooter after one year.
As we did in the previous example, let's combine the two step process into ONE step!!
Described in ONE step, we did: 590 - 0.30(580) to get the value.
If we factor this ONE step expression, we get 590(1 - 0.30) or 590(0.70).
 |

The 0.70 represents ALL of the initial amount minus 30%.
70% is the % that REMAINS!!
|

The same strategy was applied in both percent increasing and percent decreasing situations to create a ONE STEP method to solving the problem.
The only difference was that percent increase involved adding,
while the percent decrease involved subtracting.

Before we officially connect these strategies to exponential growth and decay,we need to explore one more component - "time".
In Example 1 (regarding aphids), we discovered that the percent of increase after day one could be expressed as 75(1.28). What happens if we want to continue examining time intervals for not just how many aphids after one day, but how many after each day for several days?
We will need to apply the growth factor (1.28) to the result from each previous day for the designated number of days.
Start: 75 aphids
End of day 1: 75(1.28) = 96 aphids
Now, start with 96, instead of 75:
End of day 2: 96(1.28) = 122.88 = 122 aphids
Now, start with 122.88, instead of 96:
End of day 3: 122.88(1.28) = 157.2864 = 157 aphids
and so on . . .
We know that the 96 at the end of day 1 was calculated by 75(1.28).
The day 2 calculation is 96(1.28).
Replace 96 with 75(1.28) in the day 2 calculation.
The day 2 calculation is now
75(1.28)(1.28) = 75(1.28)2
We have just tied the "time" from the problem to the "exponent" in the calculation.
Day 2 = exponent of 2.
Take another look at multiplying by 1.28 each day:
Start: 75 aphids
End of day 1: 75(1.28) = 75(1.28)1 = 96 aphids
End of day 2: 75(1.28)(1.28) = 75(1.28)2 = 122.88
End of day 3: 75(1.28)(1.28)(1.28) = 75(1.28)3 = 157.2864
and so on . . . |
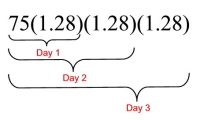 |
Do you see the connection between the exponent and the time intervals?
Day 1 = 1.281
Day 2 = 1.282 The exponent is expressing the time interval.
Day 3 = 1.283

Our strategies have now taken on an exponent
and have become the formulas for exponential growth and exponential decay.
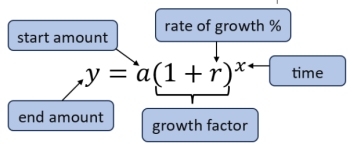
Percent of Increase (Growth)
Add Percentage |
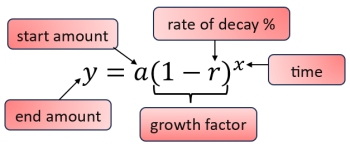
Percent of Decrease (Decay)
Subtract Percentage |
The letters used to represent the time (x) and the ending amount (y) can change based upon the terms used in a word problem.
The use of x and y used here is a reminder of which variable corresponds to which axis when graphing. |









