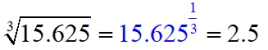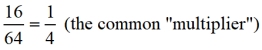|
In this lesson, we are going to discuss how to determine an exponential function
based solely upon given points, tables of values, or graphs.
The examples we will be investigating are basically "friendly" situations
(meaning that their algebraic equations are fairly easy to determine).
We will deal with "more complicated" examples in Algebra 2.
 Keep in mind that we will be looking for a function of the form y = a(b)x.
In relation to graphing, a = the y-intercept and b = the rate of growth ("multiplier").
| Find function equation given 2 points. |
 Given two "friendly" points:
QUESTION: The points (0,5) and (1,15) represent values
of an exponential function
of the
form y = a(b)x.
Find the values of a and b, and express a function passing through these points. |
SOLUTION:
The point (0,5) is graphically the y-intercept. We know that "a" represents the
y-intercept in our equation. So a = 5.
In terms of a partial equation, we now have: y = 5(b)x.
Since the point (1,15) gives us values for (x,y), we can substitute into our partial equation, and then solve for b.
y = 5(b)x
15 = 5(b)1
15 = 5b
b = 3 |
We now have all of the parts
for our function,
y = 5(3)x
|
This is a very "friendly" problem in that it supplied us with the value of a,
and made for easy calculations to find b by giving us the x-coordinate of the given point to be 1.
 Given one friendly point, and one "not quite as friendly" point:
QUESTION: The points (0,20) and (3,1280) represent values
of an exponential function
of the
form y = a(b)x.
Find the values of a and b, and express a function passing through these points.
|
SOLUTION: Again, the point (0,20) is graphically the y-intercept. We know that "a" represents the
y-intercept. So a = 20.
In terms of a partial equation, we now have: y = 20(b)x.
Since the point (3,1280) gives us values for (x,y), we can substitute into our partial equation, and then solve for b. Note: this is gong to be only a bit more challenging than Example 1.
y = 20(b)x
1280 = 20(b)3
64 = b3
b = 4 |
We now have all of the parts
for our function,
y = 20(4)x
|
This was a bit harder, but still do-able with mental calculations.
 Given one friendly point and one "not friendly" point:
QUESTION: The points (0,24) and (3,375) represent values
of an exponential function
of the
form y = a(b)x.
Find the values of a and b, and express a function passing through these points.
|
SOLUTION: Again, the point (0,24) is graphically the y-intercept. We know that "a" represents the
y-intercept. So a = 24.
In terms of a partial equation, we now have: y = 24(b)x.
Since the point (3,375) gives us values for (x,y), we can substitute into our partial equation, and then solve for b. Warning: this is gong to be a bit more challenging than Example 1.
y = 24(b)x
375 = 24(b)3
15.625 = b3
Not very nice!
b = 2.5 |
We now have all of the parts
for our function,
y = 24(2.5)x
|
 |
HOW DID WE GET 2.5???
We used the calculator!
If you studied fractional exponents, you know this fast and easy solution to find roots.
Most calculators have "keys" for square rooting
(and "menu" items for other roots).
But, if you cannot easily find the menu item for the higher roots,
here is a fast and easy hint:
To find the desired root of a number,
"raise the number to the power of 1 over the desired root".
|
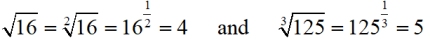
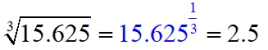
| Find function equation given a table. |
 A table easily examined.
QUESTION: Find an exponential function of the form y = a(b)x that will model the values shown in the table below.
|
SOLUTION: Start by examining the table.
As we have seen, knowing the y-intercept gives us the value for a in the equation. Look to see if the table gives you the y-intercept, (0,y).
YES. The table shows (0,1) so a = 1.
So, we have a partial equation: y = 1(b)x
|
 |
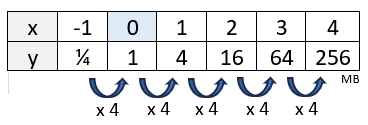Now, determine the common ratio ("multiplier") from the table. If this value is not obvious, you can find the number by dividing any y-value by the previous y-value.
For example, y = 16 divided by y = 4.
Note: always check to see that this "multiplier" applies across the entire table.
We now know b = 4. We have all of the parts for our function,
y = (4)x
 A table hiding information.
QUESTION: Find an exponential function of the form y = a(b)x that will model the values shown in the table below.
|
SOLUTION: This table is not showing us the
y-intercept, (0,y). We will need to investigate further.
Let's start by finding the common "multiplier".
Find this value by dividing any y-value by the previous y-value.
|
|
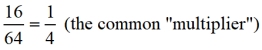
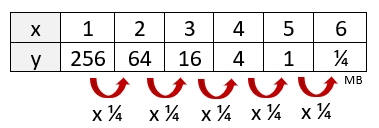
So, we have b = ¼. A partial equation is y = a(¼)x
To find a, we will work backward in the chart until we reach x = 0. When reversing the direction, we will multiply by 4 to move left in the chart. Conveniently, we only need to move one cell to the left to find x = 0. 256 x 4 = 1024 a = 1024
We have all of the parts for our function,
y = 1024(¼)x
| Find function equation given a graph. |
 A graph easily examined.
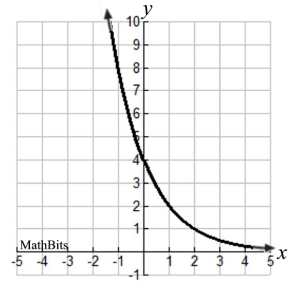
QUESTION: Find an exponential function of the
form y = a(b)x that will model the graph shown at
the right.
You may assume that there are designated points
where the graph will display integer coordinates
for both x and y (i.e. the graph has visibly
readable coordinates).
|
 |
|
SOLUTION: Start by examining the graph. Can you determine the y-intercept?
YES. The graph crosses the y-axis at (0,4). So a = 4.
So, we have a partial equation: y = 4(b)x
Look for other workable points: (1,2), (2,1) (-1,8). Making a small table may be helpful.
 
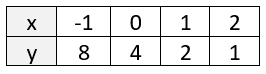
So b = ½. We have all of the parts for our function, y = 4(½)x
 A graph hiding information.
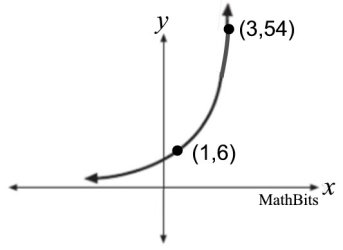
QUESTION: Find an exponential function of the
form y = a(b)x that will model the graph shown at
the right.
The only discernible points are those given:
(1,6) and (3,54). |
 |
|
SOLUTION: This graph is not going to give us any information about the y-intercept.
So, we need to be creative. Let's make a small table of what we know.
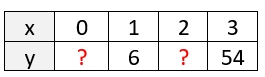
We can look at the ratio of 54/6 = 9 BUT this is the ratio over TWO INTERVALS.
Since the "multiplier" is constant, it will take TWO multiplies of some value to get to 9.
The "multiplier" must be 3. 6 x 3 = 18 18 x 3 = 54 So, b = 3.
 6 ÷ 3 = 2 And, a = 2.
So, we have all of the parts of our function. y = 2(3)x
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
