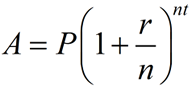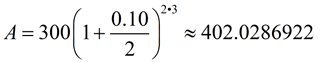|
A financial application of exponential functions deals with compound interest.
This means that we will be dealing with formulas that have a variable as an exponent.
As we examine financial interest, we will be looking at rates of growth.
There will be two exponential formulas that will be explored in this lesson.
You will learn additional information on this topic in Algebra 2.

You have already worked with the concept of "interest" in earlier grades.
You were finding simple annual interest when you used the formula I = P x r x t.
(Interest = Principal x Rate x Time)
Example: Stacey invests $300 at a simple annual interest rate of 10% for 3 years.
With simple interest, Stacey is earning $30 a year on this investment. The interest is ALWAYS based upon the original amount, not on her new yearly totals. She will continue to get the same $30 interest for each year, and the interest will be paid out at the end of each year.
End of Year 1: $300 + 0.1(300) = $330
End of Year 2: $330 + 0.1(300) = $360
End of Year 3: $360 + 0.1(300) = $390 |
Stacey's "interest" did not earn any interest
over the three year period!
At the end of 3 years,
Stacey will have $390 in her account. |
At the end of three years, Stacey will have earned $90 in interest.
I = P x R x T = 300 x 0.10 x 3 = $90.

|
A = P(1 + r)n |
Look familiar?
y = a(1 + r)x |
|
(The term "accrued" means to accumulate or to be added periodically.)
This formula will deal with a fixed annual interest rate applied once per year.
But, unlike simple interest (shown above), the compounded interest will allow for
the "interest" earned each year to be used in computing the interest for following years.
By using compound interest, your "interest" earns interest.
ALL of the money you have at the end of each year
will be used to calculate your new interest earned.
Annual Compound Interest may be called Simple Compound Interest.
|
A = accrued amount
P = Principal (starting amount)
r = interest rate
n = number of years |
|
Example: Stacey invests $300 at a fixed rate of 10% compounded annually for 3 years.
With compound interest, the "interest" Stacey earns each year is used to compute the new interest for the next year.
End of Year 1: $300 + 0.1(300) = $330
End of Year 2: $330 + 0.1(330) = $363
End of Year 3: $363 + 0.1(363) = $399.30 |
At the end of the three years, Stacey will have
A = 300(1 + 0.10)3 = 300(1.10)3 =
$399.30 in her account. |
This is exponential growth!
There is a common "multiplier" (0.1) being applied each year.

|
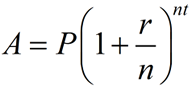 |
A = accrued
P = Principal
r = interest rate
n = number of
times per year compounded
t = time in years
|
This formula is the "generic" formula for compound interest.
It can cover "annual" compounding as well as compounding occurring more often within the year.
(If we let n = 1 in this formula, we have the same formula seen in the last section.)
This formula still deals with a fixed annual interest rate, but the interest may be applied more than simply once per year. This new formula will offer options where the investor may receive more money at the end of the invested time period.
Compounding more often will increase the interest earned.
So, this new formula will allow for multiple time periods, n,
per year, t, for the compounding to occur.
Notice in this formula that you are:
(1) dividing the rate, r, by the number of compoundings per year, n, to get the rate per each new compounding period of time, r/n, and then
(2)
raising that new growth factor, (1 + r/n) to the number of compounding periods, nt, over the entire number of years, t. |
|
The value of n when compounding:
• annual (yearly) = 1
• semi-annual = 2
• quarterly = 4
• monthly = 12
• daily = 365 |
As n grows larger, we will get more interest. |
Example: Stacey invests $300 at a fixed annual interest rate of 10% compounded every 6 months for 3 years.
As with the previous "annual compound interest" example, the "interest" which Stacey earns every 6 months is used to compute the new interest. In this formula, the fixed annual rate of 10% will be divided by 2, creating the new 6-month rate of 5%. But because this lower rate of 5% will be applied twice as often, it will yield a slight increase in the total interest acquired over the three years.
|
At the end of the three years, Stacey will have
$402.03 in her account. |
Remember, we saw in the previous example, that Stacey had $399.30 in her account at the end of 3 years by compounding only once each year. Compounding more often has given her more money.

Notice that both of the compounding formulas have variables in their exponents.
This feature makes these formulas "exponential" equations and/or functions.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|