Comparing Growth of Functions Linear, Quadratic, & Exponential MathBitsNotebook.com Topical Outline | Algebra 1 Outline | MathBits' Teacher Resources Terms of Use   Contact Person: Donna Roberts

Let's compare a linear function, a quadratic function, and an exponential function
to see how quickly they grow over time.

Start at the origin, where all 3 functions begin increasing.

• At the origin (0,0), the exponential (y = 1) exceeds the others (both y = 0).

• But, from x = 1 to x = 2, the linear exceeds the exponential and the quadratic.

• Then at x = 2, the quadratic exceeds the exponential and the linear.

So at this point, in this graph from x = 2 to x = 3, it appears that the quadratic
may be taking the lead as the function exceeding the other two functions.

Quadratic: y = x²            Linear: y = 2x           Exponential: y = 2^x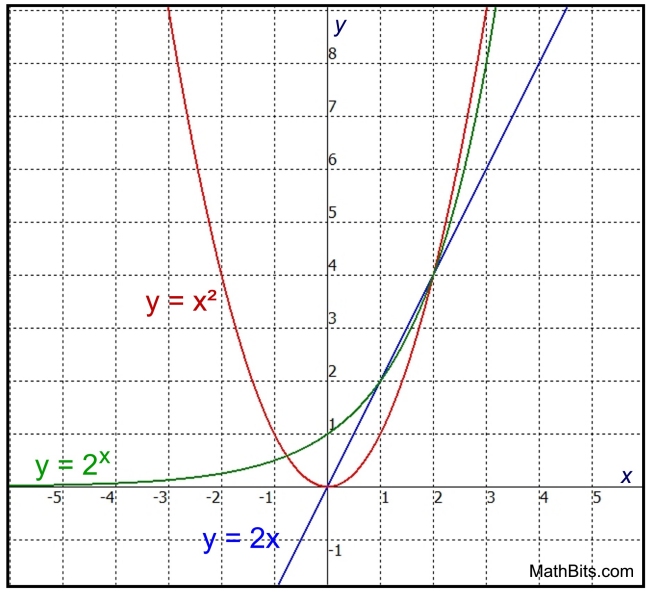

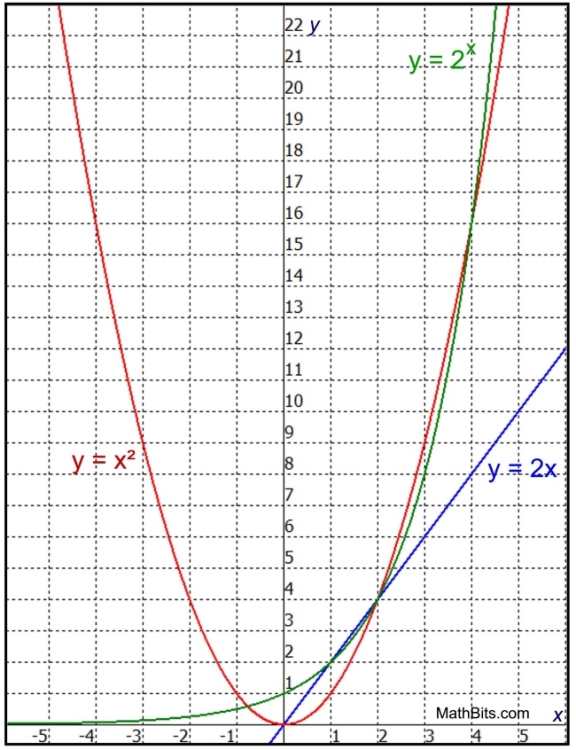
But, let's take a look at the bigger picture with a
bigger view of the y-axis.

• As we saw above, the quadratic did take the lead as the exceeding function,
but that lead only lasted from x = 2 to x = 4.

• At x = 4, the exponential function equals the quadratic function.
But, after x = 4, the exponential takes the lead.

• The exponential will hold the "lead" position from here on.

A larger graph window could be used to further verify this result.
But we know that the exponential function's average rate of change gets larger
very quickly as the x-values increase making the graph even more steep.

Still doubting?? I think we can agree that the linear function is out of the running.
Let's check a larger point for the other two functions to see what's happening.
Quadratic: At x = 20, y = x² = 20² = 400
Exponential: At x = 20, y = 2^x = 2²⁰ =1,048,576
Yep, the exponential is going to hold the lead.

Quadratic: y = x²            Linear: y = 2x           Exponential: y = 2^x

The amazing speed with which an increasing exponential function grows
overpowers the other functions.

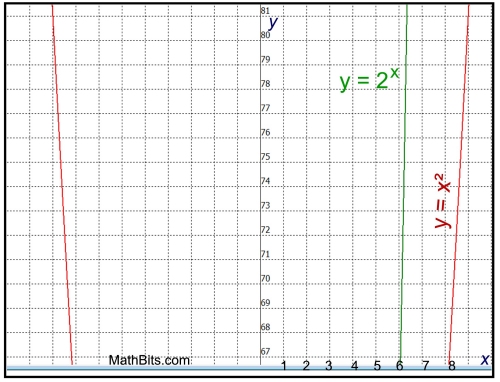
Here is a larger view of the y-axis showing that the exponential is
increasing at a rapid rate, pulling away from the quadratic.