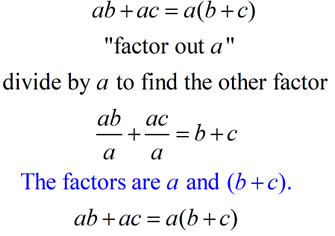|
A factor is a number or algebraic expression that divides another number or expression with no remainder. On this page, we will concentrate on finding equivalent expressions where one of the expressions is expressed in the form of a product of factors.
We will be looking specifically at "linear expressions".
 |
A linear expression is an algebraic statement where each term is either a constant or a variable raised to the first power. None of the exponents can be greater than 1.
|
|
Examples of linear expressions: 7, 3x, 2m + 5, 4x + y - 2, 2.3b - 1.2, (½)x + ¼
We will be concentrating on linear expressions that will be:
• a linear monomial (one term): an expression which has only one term and whose highest
degree is one. It does not contain any addition or subtractions signs. (Ex: 7, 3x, 3ab, 36x )
• a
linear binomial (two terms): an expression with two terms and the highest degree is one.
(Ex: 3x - 18, 2m + 5, 23ab - 2, -6x + 2y)
• a linear trinomial (three terms): an expression with three terms and the highest degree is one.
(Ex: 5x + 2y - 1, 6b - 5c - 9, -2b + 3y - 2)
(The general term of "linear polynomial" can be used for linear expressions with any number of terms.)

Distributive Property: a (b + c) = ab + ac
Distributive Property in Reverse: ab + ac = a(b + c) |
The distributive property in reverse shows the factoring of an expression.
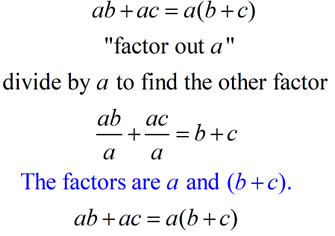
To factor an algebraic linear expression:
• Find the greatest common factor (GCF).
•
Factor out that value by dividing. |
When factoring linear expressions,
first find the GCF,
which is a factor of each term of the expression.
The GCF will be a monomial.
Factor out (divide each term by) this GCF.
The remaining factor will most likely be in parentheses.

Factor: 6x + 42
The largest integer that will divide evenly into 6 and 42 is 6. Since the terms do not contain a variable (such as x) in common, we cannot factor any variables.
The greatest common factor is 6. Divide each term by 6.
Answer: 6(x + 7)
Equivalent expressions: 6x + 42 = 6(x + 7)
|
|
Factor: 4x + 8y
The largest integer that will divide evenly into 4 and 8 is 4. Since the terms do not contain a variable (x or y) in common, we cannot factor any variables.
The GCF is 4. Divide each term by 4.
Answer: 4(x + 2y) Equivalent expressions: 4x + 8y = 4(x + 2y) |
|
Factor: (¾)a + ¼
The largest integer that divides evenly into ¾ and ¼ is ¼.
The variable a is NOT present in both terms.
The GCF is ¼. Divide each term by the GCF.
Answer: ¼ (3a + 1) Equivalent expressions: (¾)a + ¼ = ¼ (3a + 1) |
|
Factor: -12xy + 16xyw + 8xyz
The largest integer that divides evenly into 12, 16 and 8 is 4.
The variables x and y are present in all three terms.
The variable w and z are NOT present in all three terms.
The GCF is 4xy. Divide each term by the GCF.
Answer: 4xy(-3 + 4w + 2z) Equivalent expressions: -12xy + 16xyw + 8xyz = 4xy(-3 + 4w + 2z) |
|
Remember that the Distributive Property can be used in a "working backward (reverse) strategy" to express a linear expression as a product of its factors.
A linear expression is in factored form when it is expressed as the product of its factors.

|
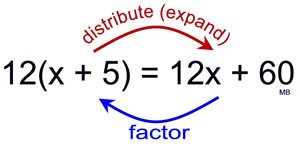
When we examine the use of the Distributive Property, in this manner, we can see that "factoring an expression" can be seen as the opposite of "distributing (expanding) an expression". |

Linear Expressions in Geometry |
The connection between factoring and the distributive property can also be seen
when dealing with area. First let's refresh a few geometry concepts that will be needed.
Consider the following concepts:
The formula for the area of a rectangle is
Area = length x width. 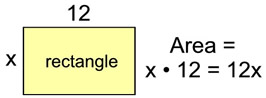 |
When dealing with line segments,
the length of a segment is
the sum (the adding) of all of its parts.
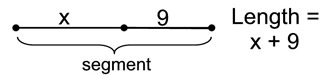
|
Now, examine the following,
where the green "box" represents a rectangle in which the dashed line forms two rectangles:
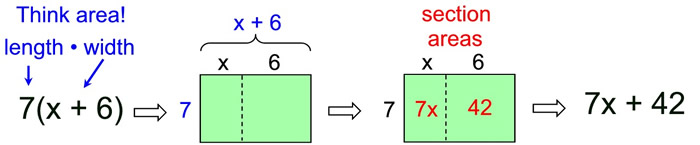
This is a visual representation of the distributive property 7(x + 6) = 7x + 42.
It can also be applied in reverse to demonstrate factoring.
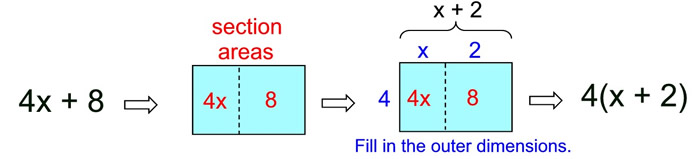
In these examples, we have seen area represented as a product, 7(x + 6) and 4(x + 2),
and area represented as a sum, 7x + 42 and 4x + 8.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|