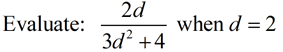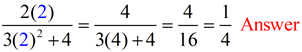hint gal
When evaluating an expression, remember to:
• place a set of parentheses around the value being substituted to help avoid errors with those pesky signed numbers.
• follow the proper rules for order of operations.

dash

Numerical Substitutions:

When working in Algebra, if a question asks you to "evaluate" a situation, you are most likely being asked to find a numerical answer. When working with algebraic expressions, the process is simple. Replace the variable(s) in the expression, with the numerical value(s) you are given, and simplify the result.

expin1
Evaluate:    x2 - 1, when x = 5.
   
Replace x with 5 and simplify.
   
(5)2 - 1 = 25 - 1 = 24 Answer
     
expin2
Evaluate:    a2b + a, when a = -3 and b = 2.
  
   
Parentheses are needed in this problem.
   
(-3)2(2) + (-3) = 18 + (-3) = 15 Answer
 

bewareS

 Do NOT write: -32(2) + (-3) as this is -9(2) + (-3) = -21
and NOT the answer.     (-3)2 does not equal -32

expin3
Evaluate:    x3 + 3x2 - 2x - 5, when x = -4.
   
Again, use parentheses to avoid errors.
   
(-4)3 + 3(-4)2 - 2(-4) - 5 = -64 + 48 + 8 - 5 = -13 Answer
   

expin4
Evaluate:    4p2 - 2p + 12, when p = -1½.
    Again, use parentheses to avoid errors.
    4(-1½)2 - 2(-1½) + 12 = 4(2¼) + 3 + 12 = 9 + 3 + 12
= 24 Answer
 

 
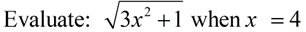expin5 evalsq
    Use parentheses to avoid errors.
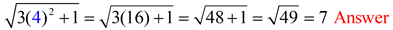    evalsq3
   

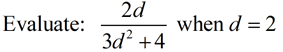expin6 evalfrac
   

Use parentheses to avoid errors.
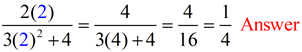    EVALFRAC2


dash

Algebraic Substitutions:

 


It may be the case that you will be asked to evaluate an expression using "another expression".
Don't panic!!! Just follow the same process as you did when evaluating for a number.
Remember to use parentheses!
expin7
Evaluate:    x2 + 2x - 4, when x = 2a.
   
Remember to use parentheses!
   
(2a)2 + 2(2a) - 4 = 4a2 + 4a - 4 Answer


   
expin8
Evaluate:   3x + 10 when x = 3m + 15
   
Remember to use parentheses!
   
3(3m + 15) + 10 = 9m + 45 + 10 = 9m + 55 Answer
   

expin9 Evaluate:   9 - 2x when x = y2 - 4
    Remember to use parentheses!
    9 - 2(y2 - 4) = 9 - 2y2 + 8 = 17 - 2y2 Answer



dash

The graphing calculator can also be used to evaluate expressions.
Click on the link at the right to see the possibilities.
ti84c
For calculator help with Evaluating Expressions
click here.

divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".