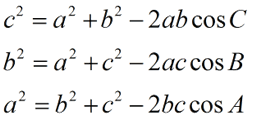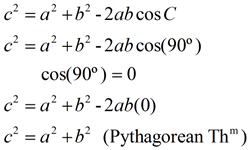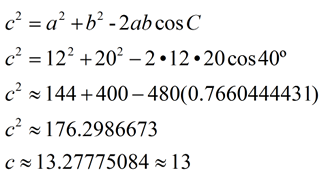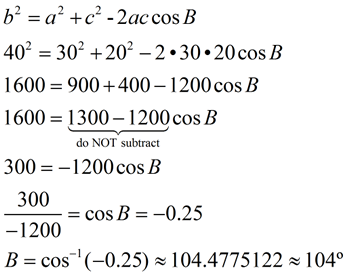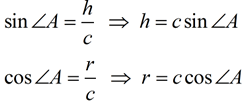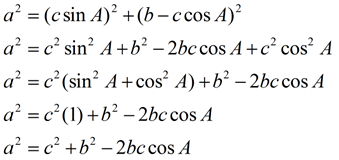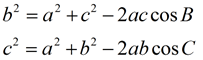|
Like the Law of Sines, the Law of Cosines lets us find missing sides and missing angles in any, and all, types of triangles. Combinations of sides and angles that could not be used in the Law of Sines, will be put to use with the Law of Cosines.
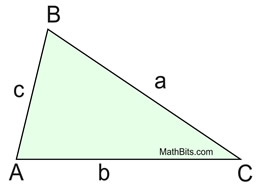
Given the diagram: |
Law of Cosines
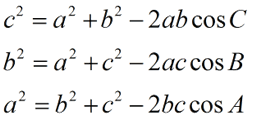
|
Notice the pattern of the letters: side c and ∠C at opposite ends of the formula, and a² with b², then 2ab. There can be a formula for each angle in the Δ. |
|
Note the lettering with
side a across from ∠A,
side b across from ∠B, and side c across from
∠C.
|
Law of Cosines in "words":
"The square of one side of the triangle is equal to the sum of the squares of the other two sides minus twice the product of the other two sides and the cosine of the angle between them."
Notice that the Law of Cosines works with only ONE angle and three sides in each formula. |
 |
You really only need to know the first formula. If your angle is not located at vertex C, simply re-label the diagram so it is located at C.
If you are asked to "Solve the triangle." (which means to find ALL of the remaining sides and angles), you may need to utilize the Law of Cosines more than once.
Did you notice how the beginning of the Law of Cosines formula contains the Pythagorean Theorem? The Law of Cosines can be thought of as a "generalization" of the Pythagorean Theorem. If angle C is a right angle (90º), the cosine of angle C will be zero, and the resulting formula becomes the Pythagorean Theorem.
 FACTS to consider about Law of Cosines and triangles: FACTS to consider about Law of Cosines and triangles:
1. In a triangle, the sum of the measures of the interior angles is 180º.
2. No triangle can have two obtuse angles.
3. In a triangle, the largest angle is opposite the longest side.
4. The proof of the Law of Cosines requires that you know that sin2A + cos2A = 1.
|
The Law of Cosines works with only one angle and three sides at a time.
As a result, the Law of Cosines can be applied only if the following combinations are given:
(1) Given two sides and the included angle, find a missing side. (Given SAS)
(2) Given three sides, find a missing angle. (Given SSS)
(3) Given two sides and the non-included angle, find a missing side. (Given SSA)
The Ambiguous Case (SSA) for the Law of Cosines will be discussed on another page.
Let's take a look at the first two situations.
Since SAS and SSS are methods of proving triangles congruent, these combinations guarantee there will be only one triangle of the given size and shape (one unique solution). |
|
SAS - Two sides and the included angle are given. |
In ΔABC, m∠C = 40º, a = 12, and b = 20.
Find side c to nearest integer.
Solution:
This problem involves all three sides of the Δ and one angle. This fits the profile of the Law of Cosines.
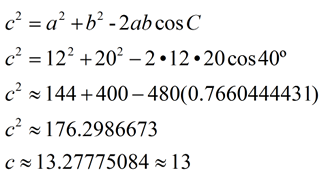 |
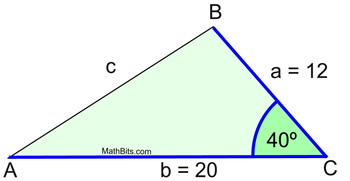
ANSWER: c = 13
Did you notice that cos 40º is positive?
When working in triangles, if an angle is acute, its cosine will be positive.
|
|
SSS - Three sides are given. |
In ΔABC, a = 30, b = 40, and c = 20.
Find the number of degrees in the largest angle
(to the nearest degree).
Solution:
The largest angle is opposite the longest side. We are looking for m∠B.
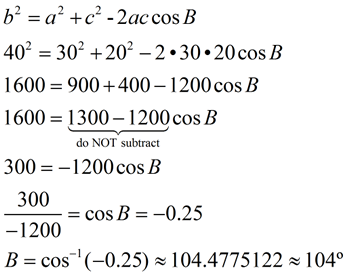 |
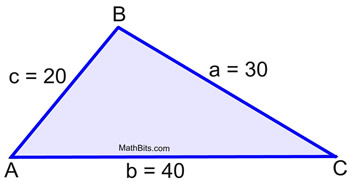
Remember that the largest angle is
opposite the longest side in a triangle..
ANSWER: m∠B = 104º
Did you notice that cos B is negative?
When working in triangles, if cosine of an angle is negative, the angle will be obtuse.
|
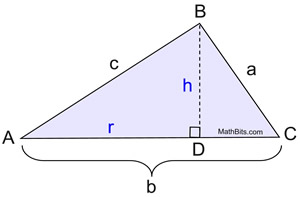
Proving the Law of Cosines: |
This proof works with an acute triangle.
Given: Δ ABC is oblique (non-right)
A perpendicular is dropped from vertex B.
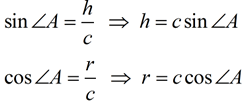 |
|
Using the Pythagorean Theorem in Δ CBD, we have a2 = h2 + ( b - r) 2.
Substituting for h and r we have:
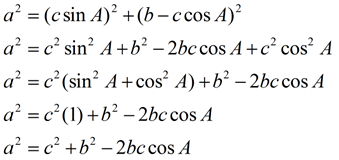
This same process can be used to produce the other lettered versions of this law:
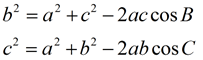
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|