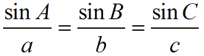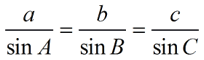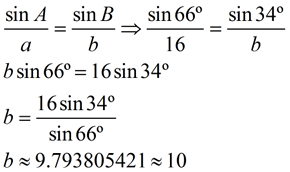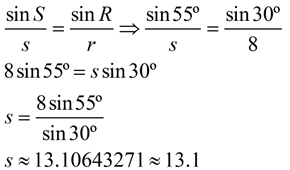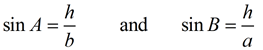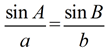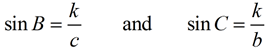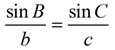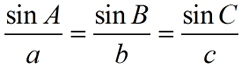|
So far, our adventure into trigonometry has been limited to working in right triangles. With a certain amount of given information about a right triangle, we have been able to find missing sides and missing angles. But can we also find missing sides and missing angles when the triangle is NOT a right triangle? What happens when the triangle is oblique?
|
An oblique triangle is any triangle that is not a right triangle. |
|
The answer to the question stated above is "yes". There are methods of finding missing sides and missing angles in oblique triangles. One such method is called the Law of Sines, which relates the lengths of the sides of any triangle to the sines of its angles.
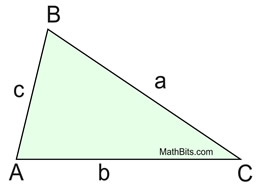
Given the diagram: |
Law of Sines
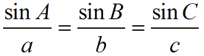
OR
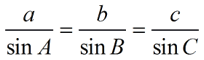
|
|
|
Note the lettering with
side a across from ∠A,
side b across from ∠B, and side c across from
∠C.
|
Law of Sines in "words":
"The ratio of the sine of an angle in a triangle to the side opposite that angle is the same for each angle in the triangle."
These equal ratios are called the Law of Sines.
Notice that the Law of Sines must work with at least two angles and two respective sides at a time. |
 |
Most problems, dealing with the Law of Sines, only require that you work with one pair of the ratios at a time. Be sure to use a pair that corresponds to your given (or known) information. If you are asked to "Solve the triangle." (which means to find ALL of the remaining sides and angles), you may need to utilize all three ratios.
|
The Law of Sines works with at least two angles and two respective sides at a time.
As a result, the Law of Sines can be applied only if certain combinations are given.
(1) Given two angles and the included side, find a missing side. (Given ASA)
(2) Given two angles and the non-included side, find a missing side. (Given AAS)
(3) Given two sides and the non-included angle, find a missing angle. (Given SSA)
The third situation is called the Ambiguous Case and will be discussed on another page.
Let's take a look at the first two situations.
Since ASA and AAS are methods of proving triangles congruent, these combinations guarantee there will be only one triangle of the given size and shape (one unique solution). |
|
|
ASA - Two angles and the included side are given. |
In ΔABC, m∠C = 80º, m∠B = 34º and a = 16.
Find side b to nearest integer.
Solution:
Since side a is given, we need the measure of ∠A.
m∠A = 180 - (m∠B + m∠C) = 180 - (34 + 80) = 66º
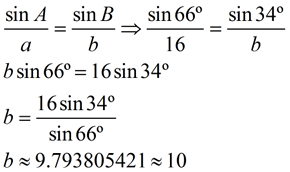
|
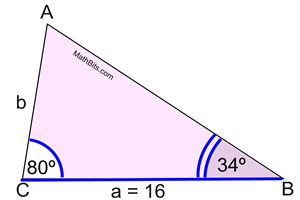
This answer makes sense, since a smaller side
is opposite a smaller angle.
ANSWER: b = 10 |
|
AAS - Two angles and the non-included side are given. |
In ΔRST, m∠R = 30º, m∠T = 95º and r = 8.
Find s to nearest tenth.
Solution:
Since we need side s, we need the measure of ∠S.
m∠S = 180 - (30 + 95) = 55º
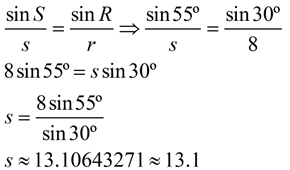
|
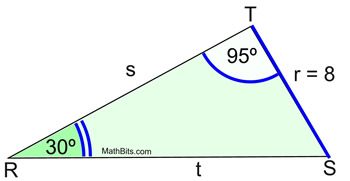
A larger side is opposite a larger angle.
ANSWER: s = 13.1
|
Proving the Law of Sines: |
This proof works with an acute triangle.
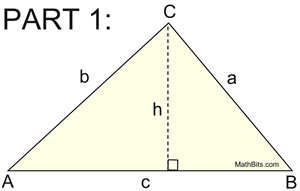
We start with an oblique (not-right) triangle ABC, with an altitude from C labeled h.
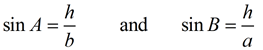
(now cross multiply)
h = b sin A and h = a sin B
(since both expressions = h)
b sin A = a sin B
(create a proportion that yields the equation above) 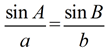
|
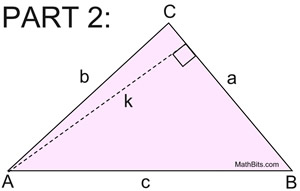
Now, draw an altitude, k, from point A.
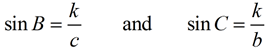
(now cross multiply)
k = c sin B and k = b sin C
(since both expressions = k)
c sin B = b sin C
(create a proportion that yields the equation above)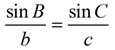
|
By combining these results, we have the Law of Sines:
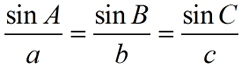
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|