Upon further investigation, however, it was discovered that there were other specific lines that also intersected in one common point inside the triangle, but these common points did not coincide with the previously found "center" point. All of the discovered common points were deemed to be "triangle centers" in the sense that each of them could be described as the center of the triangle under certain conditions.
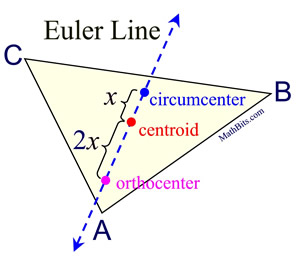
So, how many "centers" does a triangle possess? The Greeks knew of three such "centers", the centroid, the orthocenter, and the circumcenter, referred to as the classical triangle centers. Over time, mathematicians have extended the list of "triangle centers" to contain over 100 entries. It was not until the eighteenth century that mathematician Leonhard Euler (1707-1783) discovered a relationship between the three classical triangle centers. Euler discovered that in any triangle, the centroid, orthocenter and circumcenter are collinear (they lie on the same straight line).
We will start our investigation with the three classical triangle centers: the centroid, the orthocenter, and the circumcenter. We will also investigate the incenter.
Topical Outline | Geometry Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|