We will continue our investigation of the
classical triangle centers with the
circumcenter.
|
A point of concurrency is the point where three or more lines intersect. |
|
We have already seen how to circumscribe a circle about a triangle.
This discussion will focus on the name given to that point where the perpendicular bisectors
in that construction intersect. That point is called the circumcenter.
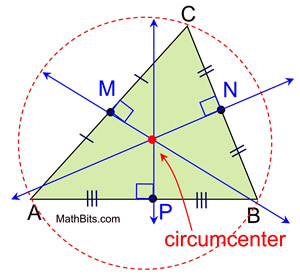
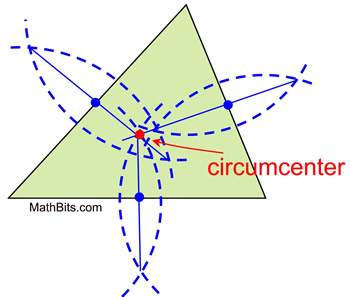
Circumcenter - point of concurrent perpendicular bisectors
The three perpendicular bisectors of the sides of a triangle are concurrent, meaning they intersect in one common point. That common point is called the circumcenter of the triangle.
We know that common point is also the center of a circumscribed circle passing through all of the vertices of the triangle. Since the radii of the circle are congruent, the center (the circumcenter) is equidistant from the vertices of the triangle.
The point of concurrency, the
circumcenter, is
not necessarily "inside" the triangle.
It may actually be
inside the triangle,
on the triangle, or
outside of the triangle.
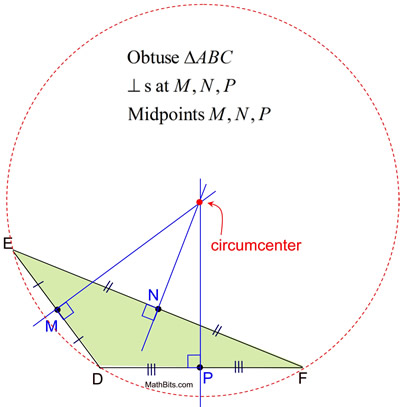
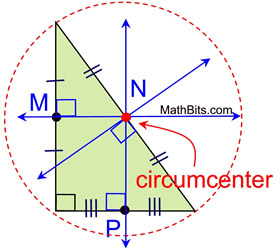
Let's take a look at the locations of the circumcenters in relation to
acute triangles (
inside),
obtuse triangles (
outside) and
right triangles (
on).
|
|
In a right triangle, the perpendicular bisectors intersect ON the hypotenuse of the triangle.
Since the center of the circumscribed circle lies on the hypotenuse, the hypotenuse becomes the diameter of the circle.
|
 |
|
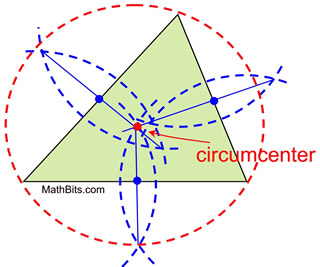
From our construction of a circumscribed circle, we know that we only really need to construct TWO of the perpendicular bisectors in a triangle to determine the point equidistant from all three vertices of the triangle. In the diagrams on this page, THREE perpendicular bisectors are shown to reinforce the definition of concurrency being "three or more" intersecting lines.
NOTE: The point of concurrency of the perpendicular bisectors of the sides of a triangle (the circumcenter) is the center of a circumscribed circle about the triangle. |
To construct the circumcenter:
Simply construct the perpendicular bisectors of the sides of the triangle.
(Actually, using only 2 sides will be sufficient to find the point.)
|
To construct the circumcircle:
Locate the circumcenter (shown at the left). Copy the length from the center to one of the vertices of the triangle. Draw the circle passing through all three vertices.
|
