|
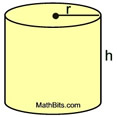
A cylinder is a three-dimensional closed figure with congruent, parallel curved bases (usually circles) connected by the set of all line segments between the two circular bases (forming a curved surface). |
The term "cylinder" is from the Greek meaning "tumbler" or "roller". |
|
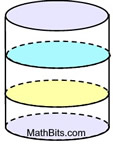
 Cross Sections Cross Sections
(parallel to bases) |
• |
A cylinder is NOT a polyhedron since it has curved surface bases (not polygons). |
• |
The bases are parallel and congruent. |
• |
The bases are circles (or curved), not polygons. |
• |
All cross sections of a cylinder parallel to the bases will be congruent to the bases. |
• |
While cylinders have several characteristics in common with prisms, they are not prisms. |
|
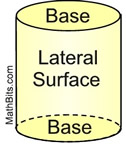
Right Circular Cylinder
|
The word "cylinder" usually refers to a cylinder whose bases are circles, resembling a tin can. A tin can is a right circular cylinder (sitting upright).
It is possible, however, for a cylinder to have congruent, parallel bases that are any curved shape, with the most popular alternative being an oval.
|
 |
| The word "cylinder" will refer to a right circular cylinder, unless otherwise stated. |
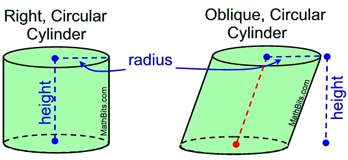 |
If the segments joining the centers of the circular bases are perpendicular to the two planes of the circles, the cylinder is called a right circular cylinder (it sits upright).
If the segments joining the center of the circles are not perpendicular to the planes of the circles, the cylinder is called an oblique circular cylinder. |

Volume of a Cylinder (for both right and oblique cylinders):
|
The volume of a cylinder is the area of its base times its height.
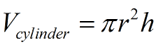 |
|
The volume of a cylinder can be calculated in the same manner as the volume of a prism:
the volume is the product of the base area times the height of the cylinder.
Note: A cylinder is not a prism since its bases are circles (not polygons).
PRISM Volume: V = Bh CYLINDER Volume: V = (πr2)h
B = area of base. Base of a cylinder is a circle. B = πr2 (for a cylinder)
Since the base of a cylinder is a circle, the formula for the area of a circle can be substituted into the prism's volume formula (V = Bh) for B, giving us V = (πr2)h. |
|
| |
|
V = volume in cubic units
r = radius of base in units
h = height in units
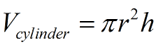
|
 |
Cylinders are commonly seen in everyday life. Food storage "cans" are one example. |
Example:
Find the volume of this right circular cylinder, to the nearest tenth of a cubic inch.
Solution:
• Notice that the diameter is given (12.4), but we need the radius, which is 6.2 inches.
• The height = 14.2 inches.
• The volume formula is V = πr2h = π • 6.22 • 14.2.
V = 1714.8 cubic inches |
|
|

Justification of formula by "stacking":
(For this discussion, our cylinder will be a right circular cylinder.)
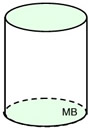
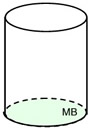
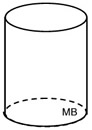
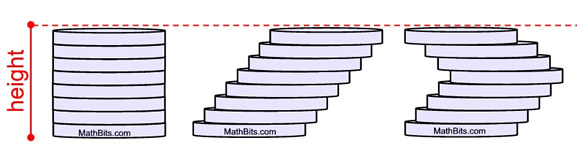
The first diagram below shows a right circular cylinder being cut into 8 congruent slices (discs) parallel to the bases. The cylinder becomes a "stacking" of congruent discs.
The volume of each disc is the same, making the total volume of the discs equal to the volume of the cylinder.
As the height of the discs becomes smaller we have a situation that looks like the second diagram below. The total of the volume of the discs still equals the volume of the cylinder, but there are many more discs in the "stack", making their height smaller.

We want to continue "stacking" discs, of smaller and smaller heights, until the height is so small that the height cannot be seen. A disc with no discernible height will start to resemble a flat 2-dimensional circle. The volume of such a disc will approach the "area" of the 2-dimensional circle, as its height approaches zero.
(This concept will be proven in Calculus with the use of integrals.)
From this "stacking technique", we can conclude that if we "stack" the area of a horizontal cross section, with a thickness so small it does not affect calculations, for the entire height of the cylinder, it will represent the volume of the cylinder.
This "stacking" gives us the "area of a circle" times the "height of the cylinder" as the volume. 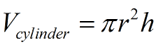

Let's look further at what that stack of disc forming a cylinder can show us:
The diagrams below show 8 congruent slices of a right circular cylinder, parallel to the bases, being "slid" to the right in two different arrangements. Since the volume of each slice is the same, the volume of all three solids the same
. 
If the number of slices is significantly increased, it can be seen that these shapes will approach the solids shown below (a right circular cylinder, an oblique circular cylinder, and a distorted solid).
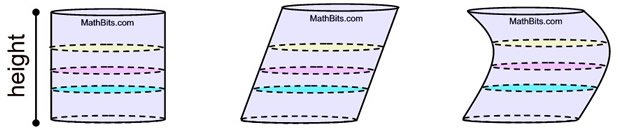
Since the heights of these three solids are the same and the areas of the cross-sections along the heights are the same, we can conclude that the volumes of all three versions are the same.
By Cavalieri's Principle, we know that if we "slice" a right circular cylinder horizontally to its bases, and then slide the sections to the right, we can form an oblique cylinder or a distorted solid of the same volume.

Surface Area of a Cylinder:
|
The surface area of a closed cylinder is a combination of the lateral area and the area of each of the bases. |
|
(For this discussion, our cylinder will be a right circular cylinder.)
When disassembled, the surface of a cylinder becomes two circular bases and a rectangular surface (lateral surface), as seen in the net at the right.
The length of the rectangular surface is the same as the circumference of the base. Remember that the area of a rectangle is its length times its width.
The lateral area (rectangle) = height x circumference of the base.
The base area = area of a circle (remember there are two bases)
Total Surface Area of a Closed Cylinder
SA = 2πrh + 2πr2
or SA =
2πr(r + h)
|
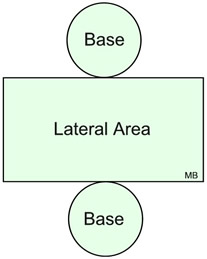 A net is a two-dimensional figure that can be cut out and folded up to make a three dimensional solid.
A net is a two-dimensional figure that can be cut out and folded up to make a three dimensional solid.
|